Question

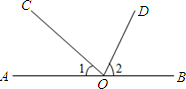
如图，AB是直线，OD，OE分别是∠AOC，∠BOC的平分线．
（1）∠BOC=72°20′，求∠1，∠2，∠DOE的度数．
（2）若∠BOC=a，求∠DOE．

Answer 1

（1）∵AB是直线，OD，OE分别是∠AOC，∠BOC的平分线．
∠BOC=72°20′，
∴∠1=∠EOB=

1

2

∠BOC=36°10′，
∴∠DOC=∠AOD=

1

2

∠AOC=

1

2

（180°-∠BOC）=

1

2

（180°-72°20′）=53°50′，
∴∠DOE=∠1+∠2=36°10′+53°50′=90°；

（2）∵AB是直线，OD，OE分别是∠AOC，∠BOC的平分线．
∴∠DOE=

1

2

∠AOC+

1

2

∠BOC=

1

2

（∠AOC+∠BOC）=

1

2

×180°=90°．