题目内容
(1)比较下列两个算式的结果的大小(在横线上选填“>”“=”或“<”)
①32+42
②(
)2+(
)2
×
;
③(-2)2+(-3)2
④(-
)2+(-
)2
)×(-
)
⑤(-4)2+(-4)2
(2)观察并归纳(1)中的规律,用含a,b的一个关系式把你的发现表示出来.
(3)若已知ab=8,且a,b都是正数,试求
a2+
b2的最小值.
①32+42
>
>
2×3×4; ②(
| 1 |
| 3 |
| 1 |
| 4 |
>
>
2×| 1 |
| 3 |
| 1 |
| 4 |
③(-2)2+(-3)2
>
>
2×(-2)×(-3);④(-
| 1 |
| 3 |
| 1 |
| 5 |
>
>
2×(-| 1 |
| 3 |
| 1 |
| 5 |
⑤(-4)2+(-4)2
=
=
2×(-4)×(-4)…(2)观察并归纳(1)中的规律,用含a,b的一个关系式把你的发现表示出来.
(3)若已知ab=8,且a,b都是正数,试求
| 1 |
| 2 |
| 1 |
| 2 |
分析:(1)①②③④⑤分别计算两个算式左右的值即可比较出大小;
(2)根据上式规律得出a2+b2≥2ab;
(3)根据a2+b2≥2ab,得出
a2+
b2的最小值为
×2ab,进而得出即可.
(2)根据上式规律得出a2+b2≥2ab;
(3)根据a2+b2≥2ab,得出
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)①∵32+42=25,2×3×4=24,
∴32+42>2×3×4;
②∵(
)2+(
)2=
,2×
×
=
,
∴(
)2+(
)2>2×
×
,
③∵(-2)2+(-3)2=4+9=13,2×(-2)×(-3)=12,
∴(-2)2+(-3)2>2×(-2)×(-3);
④∵(-
)2+(-
)2=
,2×(-
)×(-
)=
,
∴(-
)2+(-
)2>2×(-
)×(-
);
⑤∵(-4)2+(-4)2=32,2×(-4)×(-4)=32,
∴(-4)2+(-4)2=2×(-4)×(-4);
故答案为:①>,②>,③>,④>,⑤=;
(2)观察(1)中的计算可发现规律:a2+b2≥2ab;
(3)∵a2+b2的最小值是2ab,
∴
a2+
b2=
(a2+b2)=
×2ab=8.
∴32+42>2×3×4;
②∵(
| 1 |
| 3 |
| 1 |
| 4 |
| 25 |
| 144 |
| 1 |
| 3 |
| 1 |
| 4 |
| 24 |
| 144 |
∴(
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
③∵(-2)2+(-3)2=4+9=13,2×(-2)×(-3)=12,
∴(-2)2+(-3)2>2×(-2)×(-3);
④∵(-
| 1 |
| 3 |
| 1 |
| 5 |
| 34 |
| 225 |
| 1 |
| 3 |
| 1 |
| 5 |
| 30 |
| 225 |
∴(-
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
⑤∵(-4)2+(-4)2=32,2×(-4)×(-4)=32,
∴(-4)2+(-4)2=2×(-4)×(-4);
故答案为:①>,②>,③>,④>,⑤=;
(2)观察(1)中的计算可发现规律:a2+b2≥2ab;
(3)∵a2+b2的最小值是2ab,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了完全平方公式的应用,根据已知得出一般规律a2+b2≥2ab是解题关键.

练习册系列答案
相关题目
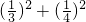 ______2×
______2×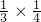 ;
;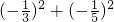 ______
______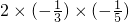
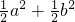 的最小值.
的最小值.