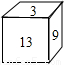
题目内容
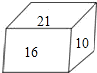 如图.正方体的每一个面上都有一个正整数,并且相对面所写的两个数的和都相等,若10的对面是数a,16的数的对面是b,21的对面是数c,则代数式(a-b)2+(b-c)2+(c-a)2的值是
如图.正方体的每一个面上都有一个正整数,并且相对面所写的两个数的和都相等,若10的对面是数a,16的数的对面是b,21的对面是数c,则代数式(a-b)2+(b-c)2+(c-a)2的值是
- A.179
- B.180
- C.181
- D.182
D
分析:根据相对面所写的两个数的和都相等可以得到三个等式,把三个等式进行适当变形然后代入代数式求值.
解答:因为正方体相对面所写的两个数的和都相等,
根据已知条件,可得10+a=16+b=21+c,
10+a=16+b?a-b=6;
10+a=21+c?c-a=-11;
16+b=21+c?b-c=5.
将它们分别代入代数式得,
(a-b)2+(b-c)2+(c-a)2
=36+25+121
=182
故选D.
点评:本题主要考查正方体的空间图形,从相对面入手,分析及解答问题.
分析:根据相对面所写的两个数的和都相等可以得到三个等式,把三个等式进行适当变形然后代入代数式求值.
解答:因为正方体相对面所写的两个数的和都相等,
根据已知条件,可得10+a=16+b=21+c,
10+a=16+b?a-b=6;
10+a=21+c?c-a=-11;
16+b=21+c?b-c=5.
将它们分别代入代数式得,
(a-b)2+(b-c)2+(c-a)2
=36+25+121
=182
故选D.
点评:本题主要考查正方体的空间图形,从相对面入手,分析及解答问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
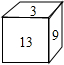 如图,正方体的每一个面上都有一个正整数,已知相对的两个面上两数之和都相等.如果13、9、3对面的数分别为a、b、c,则a2+b2+c2-ab-bc-ca的值等于( )
如图,正方体的每一个面上都有一个正整数,已知相对的两个面上两数之和都相等.如果13、9、3对面的数分别为a、b、c,则a2+b2+c2-ab-bc-ca的值等于( )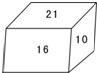 10、如图.正方体的每一个面上都有一个正整数,并且相对面所写的两个数的和都相等,若10的对面是数a,16的数的对面是b,21的对面是数c,则代数式(a-b)2+(b-c)2+(c-a)2的值是( )
10、如图.正方体的每一个面上都有一个正整数,并且相对面所写的两个数的和都相等,若10的对面是数a,16的数的对面是b,21的对面是数c,则代数式(a-b)2+(b-c)2+(c-a)2的值是( )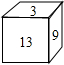 如图,正方体的每一个面上都有一个正整数,已知相对的两个面上两数之和都相等.如果13、9、3对面的数分别为a、b、c,则a2+b2+c2-ab-bc-ca的值等于
如图,正方体的每一个面上都有一个正整数,已知相对的两个面上两数之和都相等.如果13、9、3对面的数分别为a、b、c,则a2+b2+c2-ab-bc-ca的值等于