题目内容
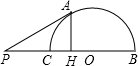如图，P是半圆O的直径BC延长线上一点，PA切半圆于点A，AH⊥BC于H，若PA=1，PB+PC=a（a＞2），则PH等于
- A.
- B.
- C.
- D.
A
分析：连接OA，构造△APH∽△OPA，通过相似比可求出PH的长．
解答：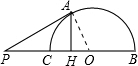
解：如图，连接OA．
∵PA2=PC•PB
又∵PC+PB=a
∴BC=PB-PC=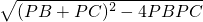
=
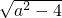
∴OA=OC=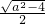
∴OP=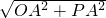
=
又∵∠APH=∠OPA，∠PAO=∠PHA=90°
∴△APH∽△OPA
∴
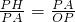
∴PH=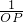
=
故选A．
点评：此题运用了切割线定理，勾股定理，相似三角形的判定、性质等有关知识．
分析：连接OA，构造△APH∽△OPA，通过相似比可求出PH的长．
解答：
解：如图，连接OA．∵PA2=PC•PB
又∵PC+PB=a
∴BC=PB-PC=
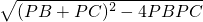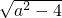
=∴OA=OC=
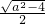
∴OP=
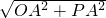=又∵∠APH=∠OPA，∠PAO=∠PHA=90°
∴△APH∽△OPA
∴
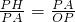
∴PH=
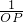=故选A．
点评：此题运用了切割线定理，勾股定理，相似三角形的判定、性质等有关知识．
练习册系列答案
相关题目
道BC的长86.96米，跑道的宽为l米．（π=3.14，结果精确到0.01）
与
，如下图
