题目内容
如图所示,直线 与y轴相交于点D,点A1在直线
与y轴相交于点D,点A1在直线 上,点B1在X轴上,且△OA1B1是正三角形,记作第一个正三角形;然后过B1作B1A2∥OA1与直线
上,点B1在X轴上,且△OA1B1是正三角形,记作第一个正三角形;然后过B1作B1A2∥OA1与直线 相交于点A2,点B2在X轴上,再以B1A2为边作正三角形A2B2B1,记作第二个正三角形;同样过B2作B2A3∥B1A2与直线
相交于点A2,点B2在X轴上,再以B1A2为边作正三角形A2B2B1,记作第二个正三角形;同样过B2作B2A3∥B1A2与直线 相交于点A3,点B3在x轴上,再以B2A3为边作正三角形A3B3B2,记作第三个正三角形;…依此类推,则第n个正三角形的顶点An的纵坐标为
相交于点A3,点B3在x轴上,再以B2A3为边作正三角形A3B3B2,记作第三个正三角形;…依此类推,则第n个正三角形的顶点An的纵坐标为
- A.2n-1
- B.2n-2
- C.

- D.

D
分析:可设直线与x轴相交于C点.通过求交点C、D的坐标可求∠DCO=30°.根据题意得△COA1、△CB1A2、△CB2A3…都是等腰三角形,且腰长变化有规律.在正三角形中求高即可得解.
解答: 解:设直线与x轴相交于C点.
解:设直线与x轴相交于C点.
令x=0,则y= ; 令y=0,则x=-1.
; 令y=0,则x=-1.
∴OC=1,OD= .
.
∵tan∠DCO= =
= ,∴∠DCO=30°.
,∴∠DCO=30°.
∵△OA1B1是正三角形,∴∠A1OB1=60°.
∴∠CA1O=∠A1CO=30°,∴OA1=OC=1.
∴第一个正三角形的高=1×sin60°= ;
;
同理可得:第二个正三角形的边长=1+1=2,高=2×sin60°= ;
;
第三个正三角形的边长=1+1+2=4,高=4×sin60°=2 ;
;
第四个正三角形的边长=1+1+2+4=8,高=8×sin60°=4 ;
;
…
第n个正三角形的边长=2(n-1),高=2(n-2)× .
.
∴第n个正三角形顶点An的纵坐标是2(n-2)× .
.
故选D.
点评:此题考查一次函数的应用及正三角形的有关计算,综合性强,难度大.
分析:可设直线与x轴相交于C点.通过求交点C、D的坐标可求∠DCO=30°.根据题意得△COA1、△CB1A2、△CB2A3…都是等腰三角形,且腰长变化有规律.在正三角形中求高即可得解.
解答:
 解:设直线与x轴相交于C点.
解:设直线与x轴相交于C点.令x=0,则y=
 ; 令y=0,则x=-1.
; 令y=0,则x=-1.∴OC=1,OD=
 .
.∵tan∠DCO=
 =
= ,∴∠DCO=30°.
,∴∠DCO=30°.∵△OA1B1是正三角形,∴∠A1OB1=60°.
∴∠CA1O=∠A1CO=30°,∴OA1=OC=1.
∴第一个正三角形的高=1×sin60°=
 ;
;同理可得:第二个正三角形的边长=1+1=2,高=2×sin60°=
 ;
;第三个正三角形的边长=1+1+2=4,高=4×sin60°=2
 ;
;第四个正三角形的边长=1+1+2+4=8,高=8×sin60°=4
 ;
;…
第n个正三角形的边长=2(n-1),高=2(n-2)×
 .
.∴第n个正三角形顶点An的纵坐标是2(n-2)×
 .
.故选D.
点评:此题考查一次函数的应用及正三角形的有关计算,综合性强,难度大.

练习册系列答案
相关题目
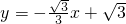 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,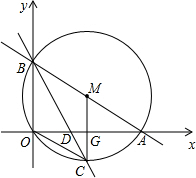 交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.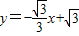 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.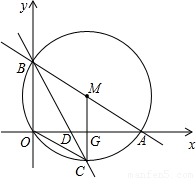
 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
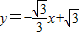 与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.
与x轴、y轴分别交于A、B两点,直线BC交x轴于D,交△ABO的外接圆⊙M于C,已知∠COD=∠OBC.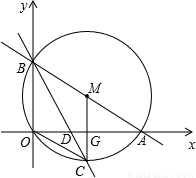
 与y轴交于点
与y轴交于点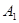 ,以
,以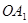 为边作正方形
为边作正方形 然后
然后 与直线
与直线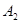 ,得到第一个梯形
,得到第一个梯形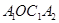 ;再以
;再以 为边作正方形
为边作正方形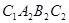 ,同样延长
,同样延长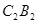 与直线
与直线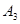 得到第二个梯形
得到第二个梯形 ;,再以
;,再以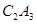 为边作正方形
为边作正方形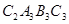 ,延长
,延长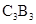 ,得到第三个梯形;……则第2个梯形
,得到第三个梯形;……则第2个梯形
 (n是正整数)个梯形的面积是
(用含n的式子
(n是正整数)个梯形的面积是
(用含n的式子