题目内容
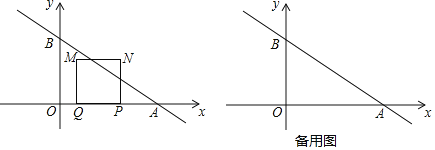
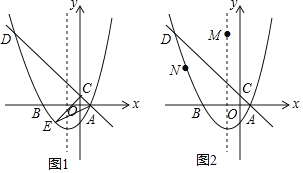
【题目】如图1，在平面直角坐标系中，直线y=-x+1与抛物线y=ax2+bx+c（a≠0）相交于点A（1，0）和点D（-4，5），并与y轴交于点C，抛物线的对称轴为直线x=-1，且抛物线与x轴交于另一点B．
（1）求该抛物线的函数表达式；
（2）若点E是直线下方抛物线上的一个动点，求出△ACE面积的最大值；
（3）如图2，若点M是直线x=-1的一点，点N在抛物线上，以点A，D，M，N为顶点的四边形能否成为平行四边形？若能，请直接写出点M的坐标；若不能，请说明理由．
【答案】（1）y=x2+2x-3；（2）△ACE的面积的最大值为
；（3）点M的坐标为（-1，26）或（-1，16）或（-1，8）.
【解析】
（1）先利用抛物线的对称性确定出点B的坐标，然后设抛物线的解析式为y=a（x+3）（x-1），将点D的坐标代入求得a的值即可；
（2）过点E作EF∥y轴，交AD与点F，过点C作CH⊥EF，垂足为H．设点E（m，m2+2m-3），则F（m，-m+1），则EF=-m2-3m+4，然后依据△ACE的面积=△EFA的面积-△EFC的面积列出三角形的面积与m的函数关系式，然后利用二次函数的性质求得△ACE的最大值即可；
（3）当AD为平行四边形的对角线时．设点M的坐标为（-1，a），点N的坐标为（x，y），利用平行四边形对角线互相平分的性质可求得x的值，然后将x=-2代入求得对应的y值，然后依据
，可求得a的值；当AD为平行四边形的边时．设点M的坐标为（-1，a）．则点N的坐标为（-6，a+5）或（4，a-5），将点N的坐标代入抛物线的解析式可求得a的值．
（1）∵A（1，0），抛物线的对称轴为x=-1，
∴B（-3，0）．
设抛物线的解析式为y=a（x+3）（x-1），
将点D的坐标代入得：5a=5，解得a=1，
∴抛物线的解析式为y=x2+2x-3．
（2）如图1所示：过点E作EF∥y轴，交AD与点F，过点C作CH⊥EF，垂足为H．
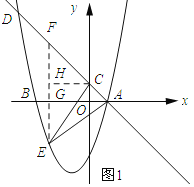
设点E（m，m2+2m-3），则F（m，-m+1）．
∴EF=-m+1-m2-2m+3=-m2-3m+4
∴△ACE的面积=△EFA的面积-△EFC的面积=
EFAG-EFHC=EFOA=-（m+
）2+．
∴△ACE的面积的最大值为．
（3）当AD为平行四边形的对角线时．
设点M的坐标为（-1，a），点N的坐标为（x，y）．
∵平行四边的对角线互相平分，
∴
，．
解得：x=-2，5-a．
将点N的坐标代入抛物线的解析式得：5-a=-3，
∴a=8．
∴点M的坐标为（/span>-1，8）．
当AD为平行四边形的边时．
设点M的坐标为（-1，a）．
∵四边形MNAD为平行四边形，
∴点N的坐标为（-6，a+5）或（4，a-5）．
∵将x=-6，y=a+5代入抛物线的解析式得：a+5=36-12-3，解得：a=16，
∴M（-1，16）．
将x=4，y=a-5代入抛物线的解析式得：a-5=16+8-3，解得：a=26，
∴M（-1，26）．
综上所述，当点M的坐标为（-1，26）或（-1，16）或（-1，8）时，以点A，D，M，N为顶点的四边形能成为平行四边形．
