题目内容
方程组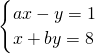 的解是
的解是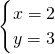 ,那么方程x2+ax+b=0
,那么方程x2+ax+b=0
- A.有两个不相等实数根
- B.有两个相等实数根
- C.没有实数根
- D.有两个根为2和3
C
分析:先求得a,b的值,然后再根据一元二次方程的根的判别式的符号判断根的情况.
解答:把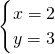 代入方程组
代入方程组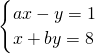 得a=2,b=2,
得a=2,b=2,
所以方程x2+ax+b=0变为x2+2x+2=0,其中a=1,b=2,c=2,
∴△=b2-4ac=22-4×1×2=-4<0,
∴方程没有实数根
故选C
点评:总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
分析:先求得a,b的值,然后再根据一元二次方程的根的判别式的符号判断根的情况.
解答:把
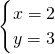 代入方程组
代入方程组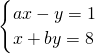 得a=2,b=2,
得a=2,b=2,所以方程x2+ax+b=0变为x2+2x+2=0,其中a=1,b=2,c=2,
∴△=b2-4ac=22-4×1×2=-4<0,
∴方程没有实数根
故选C
点评:总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
 的解是
的解是 ,那么方程x2+ax+b=0( )
,那么方程x2+ax+b=0( ) 的解是
的解是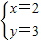 ,那么方程x2+ax+b=0( )
,那么方程x2+ax+b=0( ) 的解是
的解是 ,那么方程x2+ax+b=0( )
,那么方程x2+ax+b=0( )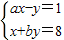 的解是
的解是 ,那么方程x2+ax+b=0( )
,那么方程x2+ax+b=0( )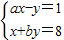 的解是
的解是 ,那么方程x2+ax+b=0( )
,那么方程x2+ax+b=0( )