题目内容
⊙O和⊙P相交于A、B两点，且两圆半径分别为5和4，公共弦AB=6，则OP=（ ）
分析：根据题意画出两种情况，根据相交两圆的性质得出OP⊥AB，根据垂径定理求出AC=3，根据勾股定理求出OC、CP，即可求出OP．
解答：解：分为两种情况：
①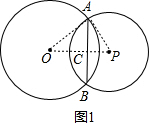
连接OA、PA、OP，OP交AB于C，
∵AB是⊙O和⊙P的公共弦，
∴OP⊥AB，
∴∠ACO=∠ACP=90°，
由垂径定理得：AC=BC=
×6=3，
由勾股定理得：OC=
=
=4，
CP=
=
，
∴OP=OC+CP=4+
；
②如图2，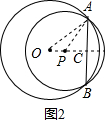
由①知：CP=
，OC=4，
∴OP=4-
，
故选D．
①
连接OA、PA、OP，OP交AB于C，
∵AB是⊙O和⊙P的公共弦，
∴OP⊥AB，
∴∠ACO=∠ACP=90°，
由垂径定理得：AC=BC=
| 1 |
| 2 |
由勾股定理得：OC=
| OA2-AC2 |
| 52-32 |
CP=
| 42-32 |
| 7 |
∴OP=OC+CP=4+
| 7 |
②如图2，
由①知：CP=
| 7 |
∴OP=4-
| 7 |
故选D．
点评：本题考查了相交两圆的性质，垂径定理，勾股定理等知识点，此题比较典型，是一道比较好但是又容易出错的题目．
练习册系列答案
相关题目
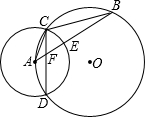已知：如图，⊙O和⊙A相交于C、D，圆心A在⊙O上，过A的直线与CD、⊙A、⊙O分别交于F、E、B．
7、如图，已知两条互相垂直的直线a和b相交于点O，试在直线a，b上找一点Q，使得△OPQ为等腰三角形，这样的点Q一共有（ ）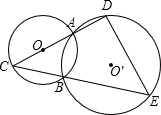
如图，⊙O和⊙O′相交于A、B两点，AC是⊙O的直径，如果AC=12，BE=30，BC=AD，则DE=
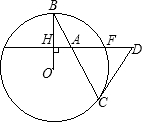如图已知OB是半径，弦EF垂直OB于H，点A是HF上的一点，BA和⊙O相交于另一点C，过点C的切线和EF的延长线交于点D：
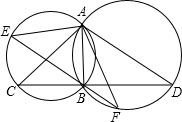如图，已知⊙M和⊙N相交于点A、B，过点B作CD⊥AB，分别交⊙M和⊙N于C、D，过点B任作一直线分别交⊙M和⊙N于E、F．