题目内容
如图,把矩形纸片OABC放入直角坐标系中,使OA,OC分别落在x轴y轴的正半轴上.连接AC,且A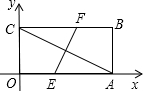 C=4
C=4| 5 |
| 1 |
| 2 |
(1)求A、C两点的坐标;
(2)求AC所在直线的函数解析式;
(3)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
分析:(1)因为AC=4
,tan∠OAC=
,∠COA=90°,所以可求出OA=2OC,利用勾股定理可得AC2=OC2+OA2,由此即可求出OC=4,OA=8,进而求出A(8,0),C(0,4);
(2)可设AC的解析式为y=kx+b,利用待定系数法即可求出AC的解析式为y=-
x+4;
(3)可设AC与EF交于点O,由折叠知EF垂直平分AC,所以O是矩形ABOC的中心,所以FO=OE,利用EF、AC互相垂直平分,可得重合部分AECF是菱形,进而可设CF=x,则AF=x,BF=8-x,因为AB=4,∠B=90°,利用勾股定理,可求出x=5,即CF=5,所以重合部分的面积=
×5×4=10.
| 5 |
| 1 |
| 2 |
(2)可设AC的解析式为y=kx+b,利用待定系数法即可求出AC的解析式为y=-
| 1 |
| 2 |
(3)可设AC与EF交于点O,由折叠知EF垂直平分AC,所以O是矩形ABOC的中心,所以FO=OE,利用EF、AC互相垂直平分,可得重合部分AECF是菱形,进而可设CF=x,则AF=x,BF=8-x,因为AB=4,∠B=90°,利用勾股定理,可求出x=5,即CF=5,所以重合部分的面积=
| 1 |
| 2 |
解答:解:(1)∵AC=4
,tan∠OAC=
,∠COA=90°,
∴
=
,即OA=2OC,
∵AC2=OC2+OA2,
∴80=OC2+4OC2,
∴OC=4,OA=8,
∴A(8,0),C(0,4);
(2)设AC的解析式为y=kx+b,
则
,
∴
,
所以AC的解析式为y=-
x+4;
(3)设:AC与EF交于点O,由折叠知EF垂直平分AC,所以O是矩形ABOC的中心,
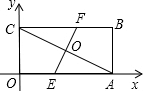
∴FO=OE,
∴EF、AC互相垂直平分,
∴重合部分AECF是菱形,
设CF=x,则AF=x,BF=8-x,
因为AB=4,∠B=90°,
∴x2=42+(8-x)2,
∴x=5,即CF=5,
∴重合部分的面积=
×5×4=10.
| 5 |
| 1 |
| 2 |
∴
| OC |
| OA |
| 1 |
| 2 |
∵AC2=OC2+OA2,
∴80=OC2+4OC2,
∴OC=4,OA=8,
∴A(8,0),C(0,4);
(2)设AC的解析式为y=kx+b,
则
|
∴
|
所以AC的解析式为y=-
| 1 |
| 2 |
(3)设:AC与EF交于点O,由折叠知EF垂直平分AC,所以O是矩形ABOC的中心,

∴FO=OE,
∴EF、AC互相垂直平分,
∴重合部分AECF是菱形,
设CF=x,则AF=x,BF=8-x,
因为AB=4,∠B=90°,
∴x2=42+(8-x)2,
∴x=5,即CF=5,
∴重合部分的面积=
| 1 |
| 2 |
点评:本题需仔细分析题意,利用勾股定理、待定系数法即可解决问题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
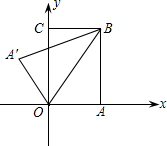 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB=
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB将纸片沿OB折叠,使A落在A′的位置,若OB= ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 
 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 

 ,tan∠BOC=
,tan∠BOC= ,则OA′=
,则OA′= 