题目内容
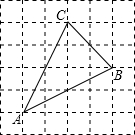（2008•临夏州）如图，网格小正方形的边长都为1．在△ABC中，试画出三边的中线（顶点与对边中点连结的线段），然后探究：三条中线位置的关系，以及三条中线所成的线段长度之间的关系，写出你发现的一般结论．分析：根据题目要求画出中线，本题中讨论的其实是三角形的重心，三角形的重心是三角形三边中线的交点，其性质之一是重心到顶点的距离与重心到对边中点的距离之比为2：1．
解答：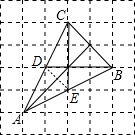
解：三条中线交于一点；
在同一条中线上，这个点到对边中点的距离等于它到顶点距离的一半．
理由：如图，三角形ABC中BD和CE分别是中线，相交于F．
连接DE．
∵DE是中位线，
∴DF：FB=DE：BC=1：2，
即重心到顶点的距离与重心到对边中点的距离之比为2：1．
解：三条中线交于一点；在同一条中线上，这个点到对边中点的距离等于它到顶点距离的一半．
理由：如图，三角形ABC中BD和CE分别是中线，相交于F．
连接DE．
∵DE是中位线，
∴DF：FB=DE：BC=1：2，
即重心到顶点的距离与重心到对边中点的距离之比为2：1．
点评：本题主要考查了三角形重心的定义和性质．一般利用相似证明重心到顶点的距离与重心到对边中点的距离之比为2：1．
练习册系列答案
相关题目
（2008•临夏州）如图，小红和小丽在操场上做游戏，她们先在地上画出一个圆圈，然后站在距圆圈5米的地方向圆圈内投小石子，则投一次就正好投到圆圈内是（ ）