题目内容
【题目】完成下面的解题过程,并在括号内填上依据.如图,EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数
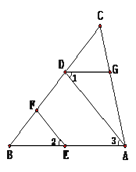
解: ∵EF∥AD,
∴∠2=____( )
又∵∠1=∠2
∴∠1=∠3
∴ ∥____( )
∴∠BAC+____=180°
∵∠BAC=85°
∴∠AGD=950
【答案】∠3;两直线平行,同位角相等;DG AB;内错角相等,两直线平行;∠AGD
【解析】试题分析:根据平行线的性质:两直线平行,同位角相等,得到∠2=∠3,再由∠1=∠2根据等量代换得到∠1=∠3,然后由平行线的判定:内错角相等,两直线平行,得到AB∥DG,再根据性质:两直线平行,同旁内角互补,可以得到∠BAC+∠AGD =180°.
试题解析:∵EF∥AD,
∴∠2=__∠3__(两直线平行,同位角相等 )
又∵∠1=∠2
∴∠1=∠3
∴AB ∥_DG ___( 内错角相等,两直线平行 )
∴∠BAC+__∠AGD __=180°
∵∠BAC=85°
∴∠AGD=950

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目