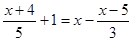题目内容
为了防控甲型H7N9流感,某校积极进行校园环境消毒,购买了甲、乙两种消毒液共100瓶,其中甲种6元/瓶,乙种9元/瓶.
(1)如果购买这两种消毒液共用780元,求甲、乙两种消毒液各购买多少瓶?
(2)该校准备再次购买这两种消毒液(不包括已购买的100瓶),使乙种瓶数是甲种瓶数的2倍,且这次所需费用不多于1200元(不包括之前的780元),求甲种消毒液最多能再购买多少瓶?
(1)如果购买这两种消毒液共用780元,求甲、乙两种消毒液各购买多少瓶?
(2)该校准备再次购买这两种消毒液(不包括已购买的100瓶),使乙种瓶数是甲种瓶数的2倍,且这次所需费用不多于1200元(不包括之前的780元),求甲种消毒液最多能再购买多少瓶?
(1)甲种消毒液购买40瓶,乙种消毒液购买60瓶;(2)50瓶
试题分析:(1)设甲种消毒液购买x瓶,则乙种消毒液购买(100-x)瓶,根据等量关系:甲消毒液总价钱+乙消毒液总价钱=780,即可列方程求解;
(2)设再次购买甲种消毒液y瓶,则购买乙种消毒液2y瓶,根据关系式:甲消毒液总价钱+乙消毒液总价钱≤1200,即可列不等式求解.
(1)设甲种消毒液购买x瓶,则乙种消毒液购买(100-x)瓶.
依题意得:6x+9(100-x)=780.
解得:x=40.
∴100-x=100-40=60(瓶).
答:甲种消毒液购买40瓶,乙种消毒液购买60瓶;
(2)设再次购买甲种消毒液y瓶,则购买乙种消毒液2y瓶.
依题意得:6y+9×2y≤1200.
解得:y≤50.
答:甲种消毒液最多再购买50瓶.
点评:解决本题的关键是读懂题意,找到符合题意的等量关系和不等关系式,正确列式求解.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
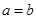 ,对于下列变形正确的是 ( )
,对于下列变形正确的是 ( )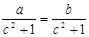
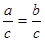

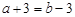
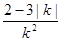 的值是 ( )
的值是 ( )