题目内容
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
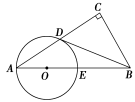
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
【答案】(1)、证明过程见解析;(2)、5.
【解析】
试题分析:(1)、连接OD,根据△AOD为等腰三角形可得∠A=∠ODA,根据∠A+∠CDB=90°可得∠ODA+∠CDB=90°,从而得出∠BDO=90°;(2)、连接OE,根据直径所对的圆周角为直角得出∠ADE=90°,根据D为中点可得E为AB的中点,根据△ADE和△ACB相似可得AC:AB=4:5,然后求出BC的长度,从而得出直径的长度.
试题解析:(1)、连接OD,在△AOD中,OA=OD, ∴∠A=∠ODA,
又∵∠A+∠CDB=90° ∴∠ODA+∠CDB=90°, ∴∠BDO=180°-90°=90°,即OD⊥BD,
∴BD与⊙O相切.
(2)、连接DE,∵AE是⊙O的直径, ∴∠ADE=90°, ∴DE∥BC.
又∵D是AC的中点,∴AE=BE. ∴△AED∽△ABC.
∴AC∶AB=AD∶AE. ∵AD:AE=4:5 ∴AC∶AB=4∶5,
令AC=4x,AB=5x,则BC=3x. ∵BC=6,∴AB=10,
∴AE=5,∴⊙O的直径为5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目