题目内容
若△ABC的边BC的垂直平分线经过顶点A,与BC相交于点D,且AB=2AD,则△ABC中必有一个内角的度数为
- A.45°
- B.60°
- C.90°
- D.120°
D
分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AB=AC,根据等边对等角可得∠B=∠C,再根据30°角所对的直角边等于斜边的一半可得∠B=30°,然后求出另外的两个内角的度数,即可得解.
解答: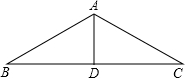 解:如图,∵边BC的垂直平分线经过顶点A,
解:如图,∵边BC的垂直平分线经过顶点A,
∴AB=AC,
∴∠B=∠C,
∵AB=2AD,
∴∠B=30°,
∴∠C=30°,∠BAC=180°-30°×2=120°,
观察各选项,只有D符合.
故选D.
点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,30°角所对的直角边等于斜边的一半的性质,作出图形更形象直观,熟记性质是解题的关键.
分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AB=AC,根据等边对等角可得∠B=∠C,再根据30°角所对的直角边等于斜边的一半可得∠B=30°,然后求出另外的两个内角的度数,即可得解.
解答:
 解:如图,∵边BC的垂直平分线经过顶点A,
解:如图,∵边BC的垂直平分线经过顶点A,∴AB=AC,
∴∠B=∠C,
∵AB=2AD,
∴∠B=30°,
∴∠C=30°,∠BAC=180°-30°×2=120°,
观察各选项,只有D符合.
故选D.
点评:本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,30°角所对的直角边等于斜边的一半的性质,作出图形更形象直观,熟记性质是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
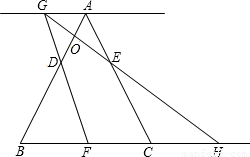
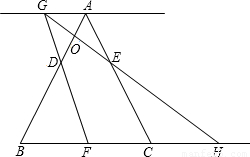
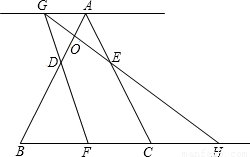
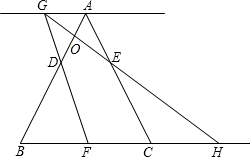 运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.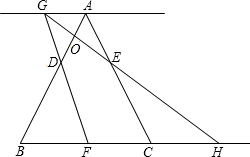 运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.