题目内容
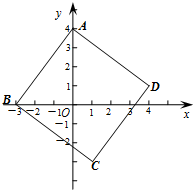14、正方形ABCD在平面直角坐标系中的位置如图所示，已知A点坐标（0，4），B点坐标（-3，0），则C点坐标（1，-3）
．分析：根据正方形的性质，过C点作CE⊥x轴于E，可证△ABO≌△BCE，求出CE，BE的长，从而求解．
解答：解：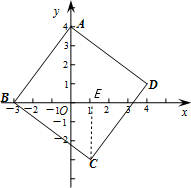
过C点作CE⊥x轴于E．
∵四边形ABCD为正方形，
∴AB=BC，∠ABC=90°，
∴∠ABO+∠CBE=90°，又∠ABO+∠BAO=90°，
∴∠BAO=∠CBE，又∠AOB=∠BEC=90°，
∴△ABO≌△BCE，
∴CE=OB=3，BE=OA=4，
∴C点坐标为（4-3，-3），即（1，-3）．
故答案为：（1，-3）．
过C点作CE⊥x轴于E．∵四边形ABCD为正方形，
∴AB=BC，∠ABC=90°，
∴∠ABO+∠CBE=90°，又∠ABO+∠BAO=90°，
∴∠BAO=∠CBE，又∠AOB=∠BEC=90°，
∴△ABO≌△BCE，
∴CE=OB=3，BE=OA=4，
∴C点坐标为（4-3，-3），即（1，-3）．
故答案为：（1，-3）．
点评：本题充分运用正方形的性质，先证△ABO≌△BCE，把已知坐标转化为相关线段的长，再求与点C的坐标有关的长度，从而确定C点坐标．
练习册系列答案
相关题目
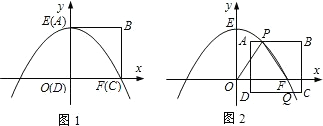如图1，在平面直角坐标系中，抛物线y=ax2+c与x轴正半轴交于点F（16，0），与y轴正半轴交于点E（0，16），边长为16的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合．
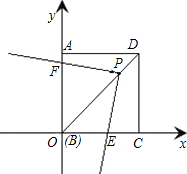如图，正方形ABCD在平面直角坐标系中的位置如图所示，点B与原点重合，点D的坐标为（4，4），当三角板直角顶点P坐标为（3，3）时，设一直角边与x轴交于点E，另一直角边与y轴交于点F．在三角板绕点P旋转的过程中，使得△POE成为等腰三角形，请写出满足条件的点F的坐标
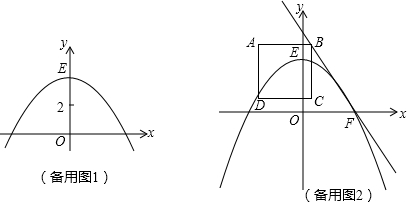
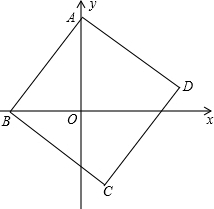（2012•和平区二模）正方形ABCD在平面直角坐标系中的位置如图所示，已知A点坐标为（0，4），B点坐标为（-3，0），则C点的坐标为（ ）