题目内容
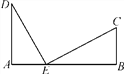
【题目】如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【答案】
(1)证明:如图1,
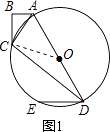
连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠C=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC= ![]() AD=r,
AD=r,
∴点C在圆O上;
(2)解:如图2,

延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB= ![]() =
= ![]() ,
,
∴tan∠CDE=tan∠ACB= ![]() ;
;
(3)解:如图3,

连结AE,作OG⊥ED于点G,则OG∥AE,且OG= ![]() AE.
AE.
易证△ABC∽△CFD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CF= ![]() ,
,
∴BF=BC+CF=8+ ![]() =
= ![]() .
.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF= ![]() ,
,
∴OG= ![]() AE=
AE= ![]() ,
,
即圆心O到弦ED的距离为 ![]() .
.
【解析】本题是圆的综合题,考查了勾股定理及其逆定理,直角三角形的性质,余角的性质,锐角三角函数定义,相似三角形的判定与性质,综合性较强,难度适中.准确作出辅助线,利用数形结合是解题的关键.(1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC= ![]() AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=
AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB= ![]() =
= ![]() ,则tan∠CDE=tan∠ACB=
,则tan∠CDE=tan∠ACB= ![]() ;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=
;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG= ![]() AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=
AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF= ![]() ,那么BF=BC+CF=
,那么BF=BC+CF= ![]() .再证明四边形ABFE是矩形,得出AE=BF=
.再证明四边形ABFE是矩形,得出AE=BF= ![]() ,所以OG=
,所以OG= ![]() AE=
AE= ![]() .
.
【考点精析】通过灵活运用实数的运算,掌握先算乘方、开方,再算乘除,最后算加减,如果有括号,先算括号里面的,若没有括号,在同一级运算中,要从左到右进行运算即可以解答此题.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案