题目内容
 已知二次函数已知二次函数y=
已知二次函数已知二次函数y=| 1 | 2 |
(1)利用配方法求出顶点坐标和对称轴;
(2)通过列表描点画出该函数图象;
(3)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?
分析:(1)用配方法求出二次函数的顶点坐标和对称轴即可;
(2)列出表格,通过顶点坐标与对称轴向左右两方取值,再描点即可得出;
(3)结合二次函数图象,即可得出二次函数的增减性性质.
(2)列出表格,通过顶点坐标与对称轴向左右两方取值,再描点即可得出;
(3)结合二次函数图象,即可得出二次函数的增减性性质.
解答:解:(1)∵y=
x2-2x-1
=
(x2-4x)-1
=
[(x2-4x+4)-4]-1
=
(x-2)2-3;
∴二次函数的顶点坐标为:(2,-3),对称轴为:x=2;
(2)①列表得:
②描点
③连线
(3)结合图象可得:x>2时,y随x的增大而增大;
x<2时,y随x的增大而减小.
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∴二次函数的顶点坐标为:(2,-3),对称轴为:x=2;
(2)①列表得:
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -1 | -2.5 | -3 | -2.5 | … |
③连线
(3)结合图象可得:x>2时,y随x的增大而增大;
x<2时,y随x的增大而减小.
点评:此题主要考查了配方法求二次函数顶点坐标与对称轴以及描点法画二次函数图象以及二次函数的性质等知识,此题是二次函数的基本性质也是考查重点,同学们应熟练掌握.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
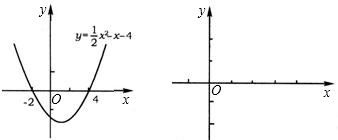
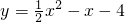 的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.
的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.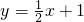 与二次函数的图象交于点A、B.
与二次函数的图象交于点A、B.
 的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.
的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______. 与二次函数的图象交于点A、B.
与二次函数的图象交于点A、B.
 的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.
的图象,填空:当函数值y>0时,x的取值范围是______;当函数值y<0时,x的取值范围是______.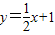 与二次函数的图象交于点A、B.
与二次函数的图象交于点A、B.