题目内容
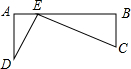如图，笔直的公路旁有A、B两车站，相距15km，C、D为同旁的两个村庄，DA⊥AB于A，CB⊥AB于B，AD=10cm，CB=5cm，要在这段公路AB旁建一个公路管理站E，使C、D两村到公路管理站的距离相等，那么公路管理站E应建在距A站________km处．
5
分析：关键描述语：在这段公路AB旁建一个公路管理站E，使C、D两村到公路管理站的距离相等，在Rt△DAE和Rt△CBE中，设出AE的长，可将DE和CE的长表示出来，列出等式进行求解即可．
解答：设AE=xkm，由勾股定理，得102+x2=52+（15-x）2，x=5．
故：E点应建在距A站5千米处．
点评：本题主要是运用勾股定理将两个直角三角形的斜边表示出来，两边相等求解即可．
分析：关键描述语：在这段公路AB旁建一个公路管理站E，使C、D两村到公路管理站的距离相等，在Rt△DAE和Rt△CBE中，设出AE的长，可将DE和CE的长表示出来，列出等式进行求解即可．
解答：设AE=xkm，由勾股定理，得102+x2=52+（15-x）2，x=5．
故：E点应建在距A站5千米处．
点评：本题主要是运用勾股定理将两个直角三角形的斜边表示出来，两边相等求解即可．
练习册系列答案
相关题目
18、如图，笔直的公路旁有A、B两车站，相距15km，C、D为同旁的两个村庄，DA⊥AB于A，CB⊥AB于B，AD=10cm，CB=5cm，要在这段公路AB旁建一个公路管理站E，使C、D两村到公路管理站的距离相等，那么公路管理站E应建在距A站
