题目内容
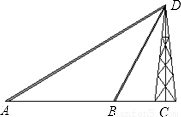
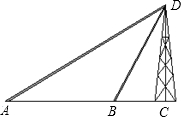 如图,有一座高60米的铁塔,需要用铁索进行固定.已知点A、B、C在同一条直线上.在A处钢索的仰角是30°,在B处钢索的仰角是60°.请求从A处到B处的距离?(结果保留3个有效数字)
如图,有一座高60米的铁塔,需要用铁索进行固定.已知点A、B、C在同一条直线上.在A处钢索的仰角是30°,在B处钢索的仰角是60°.请求从A处到B处的距离?(结果保留3个有效数字)
分析:在Rt△BCD中利用三角函数求得DB的长,再根据等角对等边即可求得AB的长.
解答:解:∵在Rt△BCD中,DC=60,∠DBC=60°.
∴sin∠DBC=
.
∴DB=40
.
∵∠DBC=60°,∠DAC=30°.
∴∠ABD=30°.
∴∠DAB=∠ADB.
∴AB=DB=40
≈69.3.
所以从A处到B处的距离是69.3米.
∴sin∠DBC=
| DC |
| DB |
∴DB=40
| 3 |
∵∠DBC=60°,∠DAC=30°.
∴∠ABD=30°.
∴∠DAB=∠ADB.
∴AB=DB=40
| 3 |
所以从A处到B处的距离是69.3米.
点评:本题主要考查了仰角的定义,一般三角形的计算可以通过作高线转化为直角三角形的计算.

练习册系列答案
相关题目
 如图甲,有一个塔高40米,位于一座山上,在其下方有一个坡度i=1:1的斜坡,某一时刻,身高1.60米的同学小明测得自己的影子(在平地上)为0.8米,那么,此时这个塔在斜坡上的影子长为多少米?(可借用图形乙)
如图甲,有一个塔高40米,位于一座山上,在其下方有一个坡度i=1:1的斜坡,某一时刻,身高1.60米的同学小明测得自己的影子(在平地上)为0.8米,那么,此时这个塔在斜坡上的影子长为多少米?(可借用图形乙)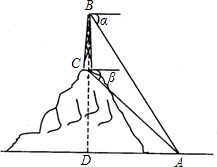 5°,已知塔高BC=60米,求山丘CD的高.(
5°,已知塔高BC=60米,求山丘CD的高.(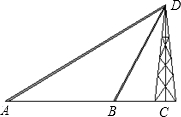 如图,有一座高60米的铁塔,需要用铁索进行固定.已知点A、B、C在同一条直线上.在A处钢索的仰角是30°,在B处钢索的仰角是60°.请求从A处到B处的距离?(结果保留3个有效数字)
如图,有一座高60米的铁塔,需要用铁索进行固定.已知点A、B、C在同一条直线上.在A处钢索的仰角是30°,在B处钢索的仰角是60°.请求从A处到B处的距离?(结果保留3个有效数字)