题目内容
【题目】如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于点C,点D在抛物线上且横坐标为3.
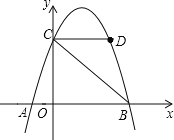
(1)求A、B、C、D的坐标;
(2)求∠BCD的度数;
(3)求tan∠DBC的值.
【答案】(1)A(﹣1,0),B(4,0),C(0,4),D(3,4);(2)45°;(3)![]() .
.
【解析】
试题分析:(1)直接利用y=0以及x=0解方程得出答案;
(2)利用(1)中所求则OC=OB=4,故∠ABC=45°,进而得出CD∥AB得出答案;
(3)过点D作DE⊥BC于点E,进而求出BE,DE的长,进而得出答案.
解:(1)令y=0,则﹣x2+3x+4=0,
即(x+1)(x﹣4)=0.
解得:x1=﹣1,x2=4.
所以A(﹣1,0),B(4,0),
令x=0,得y=4,所以C(0,4),
当x=3时,y=﹣32+3×3+4=4,
所以D(3,4);
(2)∵OC=OB=4,
∴∠ABC=45°,
∵C、D的纵坐标相同,
∴CD∥AB.
又∵OC=OB,
∴∠BCD=∠OBC=45°;
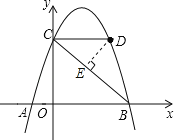
(3)过点D作DE⊥BC于点E,
在Rt△OBC中,得BC=4![]() ,
,
在Rt△CDE中,∵CD=3,
∴CE=ED=![]()
![]() ,
,
∴BE=BC﹣CE=![]()
![]() ,
,
∴tan∠DBC=![]() =
=![]() .
.

练习册系列答案
相关题目