题目内容
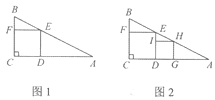
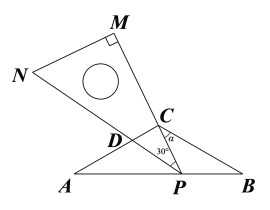
【题目】在△ABC中,CA=CB=3,∠ACB=120°,将一块足够大的直角三角尺PMN(∠M=90°,∠MPN=30°)按如图所示放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB=α,斜边PN交AC于点D.
(1)当PN∥BC时,判断△ACP的形状,并说明理由.
(2)在点P滑动的过程中,当AP长度为多少时,△ADP≌△BPC,为什么?
(3)在点P的滑动过程中,△PCD的形状可以是等腰三角形吗?若不可以,请说明理由;若可以,请直接写出α的度数.
【答案】(1)直角三角形,理由见解析;(2)当AP=3时,△ADP≌△BPC,理由见解析;(3)当α=45°或90°或0°时,△PCD是等腰三角形
【解析】
(1)由PN与BC平行,得到一对内错角相等,求出∠ACP为直角,即可得证;
(2)当AP=3时,△ADP与△BPC全等,理由为:根据CA=CB,且∠ACB度数,求出∠A与∠B度数,再由外角性质得到∠α=∠APD,根据AP=BC,利用ASA即可得证;
(3)点P在滑动时,△PCD的形状可以是等腰三角形,分三种情况考虑:当PC=PD;PD=CD;PC=CD,分别求出夹角α的大小即可.
(1)当PN∥BC时,∠α=∠NPM=30°,
又∵∠ACB=120°,
∴∠ACP=120°-30°=90°,
∴△ACP是直角三角形;
(2)当AP=3时,△ADP≌△BPC,
理由为:∵∠ACB=120°,CA=CB,
∴∠A=∠B=30°,
又∵∠APC是△BPC的一个外角,
∴∠APC=∠B+α=30°+α,
∵∠APC=∠DPC+∠APD=30°+∠APD,
∴∠APD=α,
又∵AP=BC=3,
∴△ADP≌△BPC;
(3)△PCD的形状可以是等腰三角形,
则∠PCD=120°-α,∠CPD=30°,
①当PC=PD时,△PCD是等腰三角形,
∴∠PCD=∠PDC=![]() =75°,即120°-α=75°,
=75°,即120°-α=75°,
∴∠α=45°;
②当PD=CD时,△PCD是等腰三角形,
∴∠PCD=∠CPD=30°,即120°-α=30°,
∴α=90°;
③当PC=CD时,△PCD是等腰三角形,
∴∠CDP=∠CPD=30°,
∴∠PCD=180°-2×30°=120°,
即120°-α=120°,
∴α=0°,
此时点P与点B重合,点D和A重合,
综合所述:当α=45°或90°或0°时,△PCD是等腰三角形.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】甲、乙两个商场在同一周内经营同一种商品,每天的获利情况如下表:
日期 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期天 |
甲商场获利/万元 | 2.5 | 2.4 | 2.8 | 3 | 3.2 | 3.5 | 3.6 |
乙商场获利/万元 | 1.9 | 2.3 | 2.7 | 2.6 | 3 | 4 | 4.5 |
(1)请你计算出这两个商场在这周内每天获利的平均数,并说明这两个商场本周内总的获利情况;
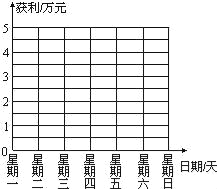
(2)在图所示的网格图内画出两个商场每天获利的折线图;(甲商场用虚线,乙商场用实线)
(3)根据折线图,请你预测下周一哪个商场的获利会多一些并简单说出你的理由.