题目内容
【题目】已知直线l:y=kx+b(k,b为常数,k≠0)与函数y=![]() 的图象交于点A(-1,m)
的图象交于点A(-1,m)
(1)求m;
(2)当k=______时,则直线l经过第一、三、四象限(任写一个符合题意的值即可);
(3)求(2)中的直线l的解析式和它与两坐标轴围成的三角形面积.
【答案】(1)m=-2;(2)1;(3)y=x-1,![]() .
.
【解析】
(1)把A(-1,m)代入y=![]() 中,便可求得m的值;
中,便可求得m的值;
(2)先把A点的坐标代入y=kx+b中,用k的代数式表示b,再根据直线直线l经过第一、三、四象限,必须满足k>0,b<0,列出k的不等式组,求得k的取值范围,便可在此取值范围中任写一个k值;
(3)求出直线l与坐标轴的交点坐标,再根据三角形的面积公式便可求得结果.
解:(1)把A(-1,m)代入y=![]() 中,得m=-2;
中,得m=-2;
(2)由(1)知,m=-2,
∴A(-1,-2),
把A(-1,-2)代入y=kx+b中,得-2=-k+b,
∴b=k-2,
∵直线l经过第一、三、四象限,
∴![]() ,
,
∴![]() ,
,
解得,0<k<2,
∴k可以取1,
故答案为1;
(3)由(2)知,k=1,b=k-2=-1,
∴直线l的解析式为:y=x-1,
∴直线l与坐标轴的交点坐标为B(0,-1),A(1,0),如图所示,
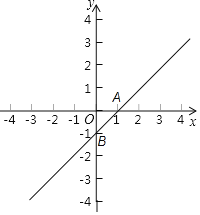
∴OA=1,OB=1,
∴![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目