题目内容
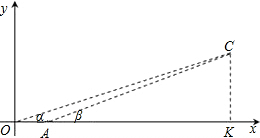
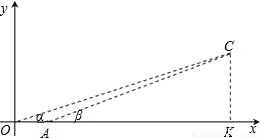
某特种侦察小队在一次作战行动中发现一个空中固定目标点C,并以O、A为两观察点,分别测得目标C的仰角分别是α和β,且tanα= ,tanβ=
,tanβ= ,又OA=1千米.
,又OA=1千米.(1)建立如图所示的平面直角坐标系,根据题中提供的数据,求出目标点C的坐标;
(2)该侦察小队及时引导武装直升机在O点正上方
 千米的D处向目标C发射了防空导弹,经测算,该导弹在离开D点的水平距离为4千米时,达到了最大的离地飞行高度3千米.若导弹飞行轨迹为抛物线,求其解析式;
千米的D处向目标C发射了防空导弹,经测算,该导弹在离开D点的水平距离为4千米时,达到了最大的离地飞行高度3千米.若导弹飞行轨迹为抛物线,求其解析式;(3)试判断按(2)中轨迹飞行的导弹是否能击中目标C,并说明理由.

【答案】分析:(1)设:CK=9t,OK=28t,AK=24t,则OA=4t,知OA长,解得t;
(2)设抛物线为:y=a(x-4)2+3,经过D点,代入解得a;
(3)当x=7时,求得y,然后作比较.
解答: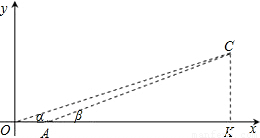 解:(1)由题意可设:CK=9t,OK=28t,AK=24t,则OA=4t,
解:(1)由题意可设:CK=9t,OK=28t,AK=24t,则OA=4t,
又∵OA=1千米,则:t=0.25,
∴OK=7,CK=2.25,(2分)
即有C的坐标(7,2.25)(1分);
(2)设抛物线为:y=a(x-4)2+3,(1分)
又经过D(0, )(1分)
)(1分)
∴ =16a+3,
=16a+3,
则:a=-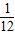 ,(2分)
,(2分)
∴抛物线为:y=-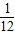 (x-4)2+3(1分);
(x-4)2+3(1分);
(3)又当x=7时代入解析式有:y=-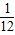 ×9+3=2.25(1分)
×9+3=2.25(1分)
∴该导弹能击中目标C.(1分)
点评:本题主要考查二次函数的应用,运用二次函数解决实际问题,比较简单.
(2)设抛物线为:y=a(x-4)2+3,经过D点,代入解得a;
(3)当x=7时,求得y,然后作比较.
解答:
 解:(1)由题意可设:CK=9t,OK=28t,AK=24t,则OA=4t,
解:(1)由题意可设:CK=9t,OK=28t,AK=24t,则OA=4t,又∵OA=1千米,则:t=0.25,
∴OK=7,CK=2.25,(2分)
即有C的坐标(7,2.25)(1分);
(2)设抛物线为:y=a(x-4)2+3,(1分)
又经过D(0,
 )(1分)
)(1分)∴
 =16a+3,
=16a+3,则:a=-
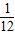 ,(2分)
,(2分)∴抛物线为:y=-
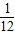 (x-4)2+3(1分);
(x-4)2+3(1分);(3)又当x=7时代入解析式有:y=-
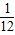 ×9+3=2.25(1分)
×9+3=2.25(1分)∴该导弹能击中目标C.(1分)
点评:本题主要考查二次函数的应用,运用二次函数解决实际问题,比较简单.

练习册系列答案
相关题目

 某特种侦察小队在一次作战行动中发现一个空中固定目标点C,并以O、A为两观察点,分别测得目标C的仰角分别是α和β,且tanα=
某特种侦察小队在一次作战行动中发现一个空中固定目标点C,并以O、A为两观察点,分别测得目标C的仰角分别是α和β,且tanα=