题目内容
如图，在平面直角坐标系中，□OABC的顶点A在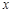
轴上，顶点B的坐标为
（6，4）．若直线l经过点（1，0），且将□OABC分割成面积相等的两部分，则直线l的函
数解析式是（ ）
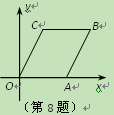
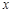轴上，顶点B的坐标为（6，4）．若直线l经过点（1，0），且将□OABC分割成面积相等的两部分，则直线l的函
数解析式是（ ）
A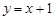． | B． |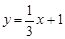
C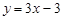． | D． |
D
析：首先根据条件l经过点D（1，0），且将?OABC分割成面积相等的两部分，求出E点坐标，然后设出函数关系式，再利用待定系数法把D，E两点坐标代入函数解析式，可得到答案．
解答：解：设D（1，0），
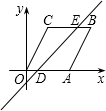
∵线l经过点D（1，0），且将?OABC分割成面积相等的两部分，
∴OD=BE=1，
∵顶点B的坐标为（6，4）．
∴E（5，4）
设直线l的函数解析式是y=kx+b，
∵图象过D（1，0），E（5，4），
∴
，
解得：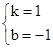
，
∴直线l的函数解析式是y=x-1．
故选D．
解答：解：设D（1，0），
∵线l经过点D（1，0），且将?OABC分割成面积相等的两部分，
∴OD=BE=1，
∵顶点B的坐标为（6，4）．
∴E（5，4）
设直线l的函数解析式是y=kx+b，
∵图象过D（1，0），E（5，4），
∴
，解得：
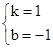，∴直线l的函数解析式是y=x-1．
故选D．
练习册系列答案
名校课堂系列答案
相关题目
与y轴交于点B，连接AB，∠a=75°，则b的值为
家与图书馆依次在一条直线上．小林、小华两人同时各自从家沿直线匀速步行到图书馆借阅图书，已知小林到达图书馆花了20分钟。设两人出发x（分钟）后，小林离小华家的距离为y（米），y与x的函数关系如图所示。
（厘米）与注水时间
（分钟）之间的关系如图2所示．根据图象提供的信息，解答下列问题：
表示________槽中水的深度与注水时间的关系，线段
表示_______槽中水的深度与注水时间之间的关系（以上两空选填“甲”或“乙”），点
的纵坐标表示的实际意义是________________________________；
中，自变量
的取值范围是 ．
