题目内容
已知,如图,已知点A的坐标是(-
,0),点B的坐标是(3
,0) ,以AB为直径作⊙M,交y轴的负半轴于点C,交y正半轴于点D,连接AC、BC,过A、B、C三点作抛物线.
,以AB为直径作⊙M,交y轴的负半轴于点C,交y正半轴于点D,连接AC、BC,过A、B、C三点作抛物线.
(1)求该抛物线的解析式;
(2)连接D M并延长交⊙M于点E,过点E作⊙M的切线分别交x轴、y轴于点F、G,求直线FG的解析式;
(3)在抛物线上是否存在这样的点P,使得以A、B、C、P为顶点的四边形是梯形?若存在,请直接写出所有满足条件的点P的坐标,若不存在,请说明理由.
| 3 |
| 3 |
 ,以AB为直径作⊙M,交y轴的负半轴于点C,交y正半轴于点D,连接AC、BC,过A、B、C三点作抛物线.
,以AB为直径作⊙M,交y轴的负半轴于点C,交y正半轴于点D,连接AC、BC,过A、B、C三点作抛物线.(1)求该抛物线的解析式;
(2)连接D M并延长交⊙M于点E,过点E作⊙M的切线分别交x轴、y轴于点F、G,求直线FG的解析式;
(3)在抛物线上是否存在这样的点P,使得以A、B、C、P为顶点的四边形是梯形?若存在,请直接写出所有满足条件的点P的坐标,若不存在,请说明理由.
分析:(1)根据点A、B的坐标求出OA、OB的长,从而得到⊙M的直径,然后求出半径DM以及OM,再根据勾股定理列式求出OD的长,根据垂径定理可得OC=OD,从而得到点C的坐标,再利用待定系数法求二次函数解析式解答;
(2)在Rt△ODM中,利用正切函数值求出∠ODM的度数是30°,再根据切线的定义可得DE⊥FG,然后解直角三角形求出DG的长度,∠DGE=60°,从而可得OG的长度,再利用∠DGE的正切函数值求出OF的长度,从而可得点G、F的坐标,再利用待定系数法求直线解析式解答即可;
(3)根据梯形的定义,分①AB是底边时,PC∥AB,利用点P的纵坐标与点C的纵坐标相等,代入抛物线解析式计算求出点P的横坐标,即可得解;②AC是底边时,PB∥AC,先根据点A、C的坐标得到直线AC的解析式,再根据平行直线的解析式的k值相等求出过点B与AC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标;③BC是底边时,AP∥BC,根据点B、C的坐标求出直线BC的解析式,再根据平行直线的解析式的k值相等求出过点A与BC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标.
(2)在Rt△ODM中,利用正切函数值求出∠ODM的度数是30°,再根据切线的定义可得DE⊥FG,然后解直角三角形求出DG的长度,∠DGE=60°,从而可得OG的长度,再利用∠DGE的正切函数值求出OF的长度,从而可得点G、F的坐标,再利用待定系数法求直线解析式解答即可;
(3)根据梯形的定义,分①AB是底边时,PC∥AB,利用点P的纵坐标与点C的纵坐标相等,代入抛物线解析式计算求出点P的横坐标,即可得解;②AC是底边时,PB∥AC,先根据点A、C的坐标得到直线AC的解析式,再根据平行直线的解析式的k值相等求出过点B与AC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标;③BC是底边时,AP∥BC,根据点B、C的坐标求出直线BC的解析式,再根据平行直线的解析式的k值相等求出过点A与BC平行的直线的解析式,然后与抛物线解析式联立求解即可得到点P的坐标.
解答:解:(1)∵点A的坐标是(-
,0),点B的坐标是(3
,0),
∴OA=
,OB=3
,
∴⊙M的直径=
+3
=4
,
∴⊙M的半径DM=
×4
=2
,
OM=2
-
=
,
在Rt△ODM中,根据勾股定理,OD=
=
=3,
根据垂径定理,OC=OD=3,
所以,点C的坐标为(0,-3),
设抛物线解析式为y=ax2+bx+c,
则
,
解得
,
所以,抛物线的解析式为y=
x2-
x-3;
(2)在Rt△ODM中,tan∠ODM=
=
,
所以,∠ODM=30°,
∵FG是⊙M的切线,
∴DE⊥FG,
∴∠DGE=90°-30°=60°,
DG=DE÷cos30°=4
÷
=8,
∴OG=DG-OD=8-3=5,
∴OF=OG•tan60°=5
,
∴点G(0,-5),F(5
,0),
设直线FG的解析式为y=kx+b,
则
,
解得
,
所以,直线FG的解析式为y=
x-5;
(3)①AB是底边时,PC∥AB,
所以,点P的纵坐标与点C的纵坐标相同,是-3,
即
x2-
x-3=-3,
整理得,x2-2
x=0,
解得x1=0(为点C坐标,舍去),x2=2
,
所以,点P的坐标为(2
,-3);
②AC是底边时,PB∥AC,由点A(-
,0)、C(0,-3)可得直线AC的解析式为y=-
x-3,
设直线PB的解析式为y=-
x+m,
把点B(3
,0)代入得,-
×3
+m=0,
解得m=9,
所以,直线PB的解析式为y=-
x+9,
联立
,
解得
(为点B的坐标,舍去),
,
所以,点P的坐标为(-4
,21);
③BC是底边时,AP∥BC,由点B(3
,0)、C(0,-3)可得直线BC的解析式为y=
x-3,
设直线AP的解析式为y=
x+n,
把点A(-
,0)代入得,
×(-
)+n=0,
解得n=1,
所以,直线AP的解析式为y=
x+1,
联立
,
解得
(为点A的坐标,舍去),
,
所以,点P的坐标为(4
,5);
经检验,三种情况时,两底边都不相等,
故存在点P(2
,-3)或(-4
,21)或(4
,5),使以A、B、C、P为顶点的四边形是梯形.
| 3 |
| 3 |
∴OA=
| 3 |
| 3 |
∴⊙M的直径=
| 3 |
| 3 |
| 3 |
∴⊙M的半径DM=
| 1 |
| 2 |
| 3 |
| 3 |
OM=2
| 3 |
| 3 |
| 3 |
在Rt△ODM中,根据勾股定理,OD=
| DM2-OM2 |
(2
|
根据垂径定理,OC=OD=3,
所以,点C的坐标为(0,-3),
设抛物线解析式为y=ax2+bx+c,
则
|
解得
|
所以,抛物线的解析式为y=
| 1 |
| 3 |
2
| ||
| 3 |
(2)在Rt△ODM中,tan∠ODM=
| OM |
| OD |
| ||
| 3 |
所以,∠ODM=30°,
∵FG是⊙M的切线,
∴DE⊥FG,
∴∠DGE=90°-30°=60°,
DG=DE÷cos30°=4
| 3 |
| ||
| 2 |
∴OG=DG-OD=8-3=5,
∴OF=OG•tan60°=5
| 3 |
∴点G(0,-5),F(5
| 3 |
设直线FG的解析式为y=kx+b,
则
|
解得
|
所以,直线FG的解析式为y=
| ||
| 3 |
(3)①AB是底边时,PC∥AB,
所以,点P的纵坐标与点C的纵坐标相同,是-3,
即
| 1 |
| 3 |
2
| ||
| 3 |
整理得,x2-2
| 3 |
解得x1=0(为点C坐标,舍去),x2=2
| 3 |
所以,点P的坐标为(2
| 3 |
②AC是底边时,PB∥AC,由点A(-
| 3 |
| 3 |
设直线PB的解析式为y=-
| 3 |
把点B(3
| 3 |
| 3 |
| 3 |
解得m=9,
所以,直线PB的解析式为y=-
| 3 |
联立
|
解得
|
|
所以,点P的坐标为(-4
| 3 |
③BC是底边时,AP∥BC,由点B(3
| 3 |
| ||
| 3 |
设直线AP的解析式为y=
| ||
| 3 |
把点A(-
| 3 |
| ||
| 3 |
| 3 |
解得n=1,
所以,直线AP的解析式为y=
| ||
| 3 |
联立
|
解得
|
|
所以,点P的坐标为(4
| 3 |
经检验,三种情况时,两底边都不相等,
故存在点P(2
| 3 |
| 3 |
| 3 |
点评:本题考查了二次函数综合题型,主要涉及待定系数法求函数解析式(包括二次函数解析式与一次函数解析式),勾股定理的应用,垂径定理,两平行直线的解析式的k值相等的性质,联立两函数解析式求交点坐标,梯形的两底边平行,(3)要分AB、AC、BC分别是底边三种情况讨论求解.

练习册系列答案
相关题目
 图象上,点C在函数
图象上,点C在函数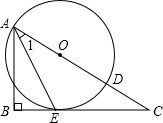 (2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
(2013•常州模拟)如图,已知点O为Rt△ABC斜边上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.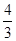 x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.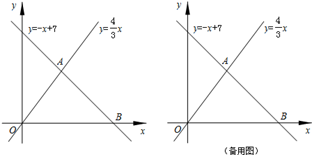
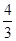 x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.