Question

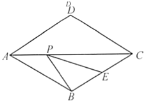
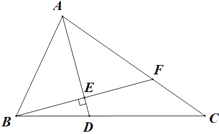
【题目】如图，在△ABC中，∠ABC=65°，∠C=35°，AD是△ABC的角平分线.

(1)求∠ADC的度数.

(2)过点B作BE⊥AD于点E，BE延长线交AC于点F.求∠AFE的度数.

Answer 1

【答案】(1)ADC=105°；(2)AFE=50°；

【解析】

（1）因为∠ABC=65°，∠C=35°，

根据三角形内角和，

可得∠BAC=80°，

由于AD是△ABC的角平分线，

则∠CAD=40°，

根据三角形的内角和可得

∠ADC=180°-∠C=35°∠CAD=40°=105°.

（2）由（1）可知∠ADC=105°，

因为BE⊥AD，

所以∠BED=∠AEF=90°，

根据三角形的内角和，

可得∠AFE=180°-∠AEF-∠CAD=50°.

（1）根据三角形内角和，结合题意可得∠BAC，再由三角形内结合以及AD是△ABC的角平分线求出答案；

（2）由（1）可知∠ADC的度数，因为BE⊥AD，所以∠BED=∠AEF=90°，再由三角形的内角和性质即可求解.