题目内容
已知多项式-2x2y3-4中,含字母的项的系数记为a,多项式的次数记为b,常数项记为c,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在如图所示的数轴上标出A,B,C:
(2)若甲,乙,丙三个动点分别从A,B,C三点同时出发沿数轴负方向运动,它们的速度分别为2、3、
(单位长度/秒),请问经过多少秒乙追上了丙?此时甲是否追上了丙?(要求有具体的解题过程)
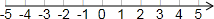
(1)求a,b,c的值,并在如图所示的数轴上标出A,B,C:
(2)若甲,乙,丙三个动点分别从A,B,C三点同时出发沿数轴负方向运动,它们的速度分别为2、3、
| 3 | 4 |
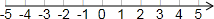
分析:(1)根据a、b、c的意义分别计算出答案即可,然后再在数轴上标出A,B,C;
(2)首先设经过x秒乙追上丙,根据题意可得乙x秒的路程为3x,丙x秒的路程为
x,根据等量关系乙的路程=丙的路程+9,由等量关系列出方程3x=9+
x,解方程可得x的值.
(2)首先设经过x秒乙追上丙,根据题意可得乙x秒的路程为3x,丙x秒的路程为
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:(1)a=-2,b=2+3=5,c=-4;
 ;
;
(2)设经过x秒乙追上丙,由题意得:
3x=9+
x,
解得:x=4,
故经过4秒乙追上丙,
(2-
)×4=5>2,
所以此时甲已经追上了丙.
 ;
;(2)设经过x秒乙追上丙,由题意得:
3x=9+
| 3 |
| 4 |
解得:x=4,
故经过4秒乙追上丙,
(2-
| 3 |
| 4 |
所以此时甲已经追上了丙.
点评:此题主要考查了一元一次方程的应用,以及数轴,关键是正确理解题意,找出题目中的等量关系,列出方程.

练习册系列答案
相关题目