题目内容
下列各题中,分解因式正确的是
- A.b(a-4)-c(4-a)=(a-4)(b-c)
- B.x2(x-2)2+2x(x-2)2=(x-2)2(x2+2x)
- C.(a-b)(a-c)+(b-a)(b-c)=(a-b)(a+b-2c)
- D.5a(x-y)+10b(y-x)=5(x-y)(a-2b)
D
分析:根据公因式的定义,对各选项提取公因式后整理即可.
解答:A、应为b(a-4)-c(4-a),
=b(a-4)+c(a-4),
=(a-4)(b+c),故本选项错误
B、应为x2(x-2)2+2x(x-2)2,
=x(x-2)2(x+2),故本选项错误;
C、应为(a-b)(a-c)+(b-a)(b-c),
=(a-b)(a-c-b+c),
=(a-b)2,故本选项错误;
D、5a(x-y)+10b(y-x),
=5(x-y)(a-2b),正确.
故选D.
点评:本题考查了提公因式法分解因式,把互为相反数的因式化为同一因式时,要注意符号的变化.
分析:根据公因式的定义,对各选项提取公因式后整理即可.
解答:A、应为b(a-4)-c(4-a),
=b(a-4)+c(a-4),
=(a-4)(b+c),故本选项错误
B、应为x2(x-2)2+2x(x-2)2,
=x(x-2)2(x+2),故本选项错误;
C、应为(a-b)(a-c)+(b-a)(b-c),
=(a-b)(a-c-b+c),
=(a-b)2,故本选项错误;
D、5a(x-y)+10b(y-x),
=5(x-y)(a-2b),正确.
故选D.
点评:本题考查了提公因式法分解因式,把互为相反数的因式化为同一因式时,要注意符号的变化.

练习册系列答案
相关题目
下列各题中,从左边到右边的变形,哪些是因式分解,哪些不是.
|
(1) |
( ) |
|
(2) |
( ) |
|
(3) |
( ) |
|
(4) |
( ) |
|
(5) |
( ) |
 .
.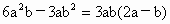 .
. .
. .
. .
.