题目内容
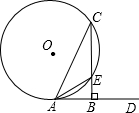 (1997•上海)如图,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,求△ABC各边的长.
(1997•上海)如图,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE=2,求△ABC各边的长.分析:由AD是⊙O的切线,根据弦切角定理,可得∠BAE=∠C,又由AE平分∠CAB,过C作AD的垂线,垂足为B,可求得∠C=∠CAE=∠BAE=30°,然后利用三角函数,求得答案.
解答:解:∵AD是⊙O的切线,
∴∠BAE=∠C,
∵AE平分∠CAB,
∴∠BAE=∠CAE,
∴∠C=∠CAE=∠BAE,
∵BC⊥AD,
∴∠ABC=90°,
∴∠C=∠CAE=∠BAE=30°,
∵AE=2,
∴在Rt△BAE中,AB=AE•cos30°=2×
=
,
∴在Rt△ABC中,AC=2AB=2
,BC=
=3.
∴△ABC各边的长分别为:AB=
,AC=2
,BC=3.
∴∠BAE=∠C,
∵AE平分∠CAB,
∴∠BAE=∠CAE,
∴∠C=∠CAE=∠BAE,
∵BC⊥AD,
∴∠ABC=90°,
∴∠C=∠CAE=∠BAE=30°,
∵AE=2,
∴在Rt△BAE中,AB=AE•cos30°=2×
| ||
| 2 |
| 3 |
∴在Rt△ABC中,AC=2AB=2
| 3 |
| AB |
| tan30° |
∴△ABC各边的长分别为:AB=
| 3 |
| 3 |
点评:此题考查了切线的性质、弦切角定理以及三角函数等知识.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
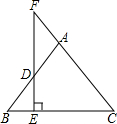 (1997•上海)如图,已知在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F,
(1997•上海)如图,已知在△ABC中,AB=AC,D是AB上一点,DE⊥BC,E是垂足,ED的延长线交CA的延长线于点F,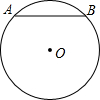 (1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是
(1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是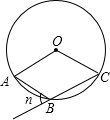 (1997•上海)如图,在⊙O中,A、B、C分别为圆周上的三点,∠ABC的补角的度数为n,那么∠AOC的度数为( )
(1997•上海)如图,在⊙O中,A、B、C分别为圆周上的三点,∠ABC的补角的度数为n,那么∠AOC的度数为( )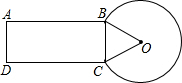 (1997•上海)如图,一种零件的横截面积是由矩形、三角形和扇形组成,矩形的长AB=2.45cm,扇形所在的圆的半径OB=1cm,扇形的弧所对的圆心角为300°,求这种零件的横截面的面积.(精确到0.01cm2,π≈3.142,
(1997•上海)如图,一种零件的横截面积是由矩形、三角形和扇形组成,矩形的长AB=2.45cm,扇形所在的圆的半径OB=1cm,扇形的弧所对的圆心角为300°,求这种零件的横截面的面积.(精确到0.01cm2,π≈3.142,