题目内容
若(4xy)•M=12x2y3-16x3y2+4x2y2,则多项式M=
3xy2-4x2y+xy
3xy2-4x2y+xy
?分析:根据已知得出M=(12x2y3-16x3y2+4x2y2)÷4xy,根据多项式除以单项式法则求出即可.
解答:解:∵(4xy)•M=12x2y3-16x3y2+4x2y2,
M=(12x2y3-16x3y2+4x2y2)÷4xy
=3xy2-4x2y+xy,
故答案为:3xy2-4x2y+xy.
M=(12x2y3-16x3y2+4x2y2)÷4xy
=3xy2-4x2y+xy,
故答案为:3xy2-4x2y+xy.
点评:本题考查了整式的除法的应用,关键是得出算式M=(12x2y3-16x3y2+4x2y2)÷4xy.

练习册系列答案
相关题目
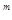 y
y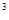 与2y
与2y 是同类项,则m-n= 。
是同类项,则m-n= 。 y
y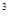 与2y
与2y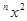 是同类项,则m-n=
。
是同类项,则m-n=
。 y
y 与2y
与2y 是同类项,则m-n= 。
是同类项,则m-n= 。