题目内容
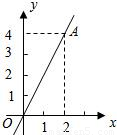
 (2008•上海)如图,在平面直角坐标系中,O为坐标原点.二次函数y=-x2+bx+3的图象经过点A(-1,0),顶点为B.
(2008•上海)如图,在平面直角坐标系中,O为坐标原点.二次函数y=-x2+bx+3的图象经过点A(-1,0),顶点为B.(1)求这个二次函数的解析式,并写出顶点B的坐标;
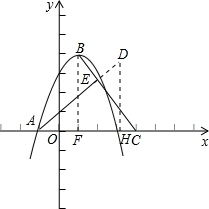
(2)如果点C的坐标为(4,0),AE⊥BC,垂足为点E,点D在直线AE上,DE=1,求点D的坐标.
分析:(1)将点A的坐标代入,可得出b的值,从而求出函数解析式,然后可得出顶点坐标;
(2)过点B作BF⊥x轴,垂足为点F,过点D作DH⊥x轴,垂足为点H.由题意知,点H在点A的右侧,则可得出△ADH∽△ACE,从而有
=
=
,然后分别讨论,①若点D在AE的延长线上,则AD=5,解出x和y的值,若点D在线段AE上,则AD=3,同理也可求出点D的坐标.
(2)过点B作BF⊥x轴,垂足为点F,过点D作DH⊥x轴,垂足为点H.由题意知,点H在点A的右侧,则可得出△ADH∽△ACE,从而有
| AH |
| AE |
| DH |
| CE |
| AD |
| AC |
解答:解:(1)∵二次函数y=-x2+bx+3的图象经过点A(-1,0),
∴0=-1-b+3,
解得:b=2,
所求二次函数的解析式为y=-x2+2x+3,
则这个二次函数图象顶点B的坐标为(1,4);
(2)过点B作BF⊥x轴,垂足为点F,
在Rt△BCF中,BF=4,CF=3,BC=5,
∴sin∠BCF=
,
在Rt△ACE中,sin∠ACE=
,
又∵AC=5,可得
=
,
∴AE=4,
过点D作DH⊥x轴,垂足为点H.由题意知,点H在点A的右侧,
易证△ADH∽△ACE,
∴
=
=
,
其中CE=3,AE=4,
设点D的坐标为(x,y),则AH=x+1,DH=y,
①若点D在AE的延长线上,则AD=5,
得
=
=
,
∴x=3,y=3,
所以点D的坐标为(3,3);
②若点D在线段AE上,则AD=3.

得
=
=
,
∴x=
,y=
,所以点D的坐标为(
,
).
综上所述,点D的坐标为(3,3)或(
,
).
∴0=-1-b+3,
解得:b=2,
所求二次函数的解析式为y=-x2+2x+3,
则这个二次函数图象顶点B的坐标为(1,4);
(2)过点B作BF⊥x轴,垂足为点F,
在Rt△BCF中,BF=4,CF=3,BC=5,
∴sin∠BCF=
| 4 |
| 5 |
在Rt△ACE中,sin∠ACE=
| AE |
| AC |
又∵AC=5,可得
| AE |
| 5 |
| 4 |
| 5 |
∴AE=4,
过点D作DH⊥x轴,垂足为点H.由题意知,点H在点A的右侧,
易证△ADH∽△ACE,
∴
| AH |
| AE |
| DH |
| CE |
| AD |
| AC |
其中CE=3,AE=4,
设点D的坐标为(x,y),则AH=x+1,DH=y,
①若点D在AE的延长线上,则AD=5,

得
| x+1 |
| 4 |
| y |
| 3 |
| 5 |
| 5 |
∴x=3,y=3,
所以点D的坐标为(3,3);
②若点D在线段AE上,则AD=3.

得
| x+1 |
| 4 |
| y |
| 3 |
| 3 |
| 5 |
∴x=
| 7 |
| 5 |
| 9 |
| 5 |
| 7 |
| 5 |
| 9 |
| 5 |
综上所述,点D的坐标为(3,3)或(
| 7 |
| 5 |
| 9 |
| 5 |
点评:此题属于二次函数综合题,涉及了待定系数法求函数解析式、相似三角形的判定与性质,解答本题的难点是第二问,关键是分类讨论,注意不要漏解,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2008•上海)如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
(2008•上海)如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( ) (2008•上海)如图,在平行四边形ABCD中,如果
(2008•上海)如图,在平行四边形ABCD中,如果