题目内容
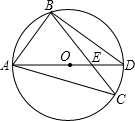（2012•崇安区一模）如图，AD为⊙O的直径，∠ABC=75°，且AC=BC．则∠BDE=30°
30°
．分析：圆周角定理得出∠ACB=∠BDE，再根据等腰三角形的性质及三角形内角和定理求出∠ACB的度数即可．
解答：解：∵∠ACB与∠BDE是
所对的圆周角，
∴∠ACB=∠BDE，
∵∠ACB=∠BDE，
∴∠BAC=∠ABC=75°，
∴∠ACB=180°-∠BAC-∠ABC=180°-2×75°=30°，
∴∠BDE=30°．
故答案为：30°．
 |
| AB |
∴∠ACB=∠BDE，
∵∠ACB=∠BDE，
∴∠BAC=∠ABC=75°，
∴∠ACB=180°-∠BAC-∠ABC=180°-2×75°=30°，
∴∠BDE=30°．
故答案为：30°．
点评：本题考查的是圆周角定理及等腰三角形的性质、三角形内角和定理，解答此类问题时要注意三角形内角和为180°这一关键知识点．
练习册系列答案
相关题目
