题目内容
追求真理是人类永恒的目标. 数学不仅要回答“什么是数学真理”,还必须回答“为什么”它是数学真理. 为了证明数学真理,就需要证明,证明就是用人人皆同意的一些“公理”与规定名词的意义,把我们以前仅凭直观或实验探索发现过的结论成为公理的逻辑推论,这样就有很强的说服力. 请你在以下2个命题中任选一个加以逻辑证明,并在你选证的命题前面括号内打“∨”.
(∨)命题1:一组对边平行且相等的四边形是平行四边形;
命题2:梯形的中位线平行于两底且等于两底和的一半.
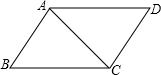 已知:在四边形ABCD中AB∥CD,AB=CD,
已知:在四边形ABCD中AB∥CD,AB=CD,求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠BAD=∠DCA,
又AB=CD AC=AC,
∴△ABC≌△CDA(SAS),
∴BC=DA,
∴四边形ABCD有两组对边相等,它是平行四边形.
分析:命题的证明一般步骤是画出图形,根据图写出已知,求证,然后根据学过的定理进行证明.
点评:本题考查命题的证明,命题证明要画图,写出已知、求证、然后进行证明.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目