题目内容
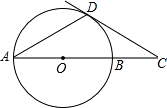 如图,在⊙O中,AB为直径,AD为弦,过D点的直线与AB的延长线交于点C.
如图,在⊙O中,AB为直径,AD为弦,过D点的直线与AB的延长线交于点C.
(1)若∠A=25°,∠C=40°,求证:CD是⊙O的切线;
(2)当∠A与∠C满足什么关系时,直线CD与⊙O相切.请直接写出你得到的结论;
(3)若CD是⊙O的切线,且AB=14,BC:DC=3:4,求OC的长.
 解:(1)证明:连接OD,
解:(1)证明:连接OD,∵OA=OD,
∴∠B=∠ADO=25°,
∴∠DOC=25°+25°=50°,
∴∠ODC=180°-∠C-∠DOC=90°,
∴CD是⊙O的切线.
(2)当2∠A+∠C=90°时,直线CD与⊙O相切.
(3)设DC=4x,BC=3x,
由切割线定理得:(4x)2=3x(3x+14),
∴x=6,
∴OC=3x+7=25,
答:OC的长是25.
分析:(1)连接OD,根据三角形外角性质求出∠AOC,根据三角形内角和定理求出∠OAC即可;
(2)根据2∠A+∠C=90°求出∠C=30°,根据三角形的内角和定理求出∠OAC的度数即可;
(3)设AC=4x,FC=3x,由切割线定理得到(4x)2=3x(3x+14),求出方程的解即可.
点评:本题主要考查对三角形的内角和定理,等腰三角形的性质,三角形的外角性质,切线的性质和判定,解一元二次方程等知识点的连接和掌握,熟练地运用这些性质进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G. 如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为
如图,在△ABC中,AB=AC,D为BC边上一点,且∠BAD=30°,若AD=DE,∠EDC=33°,则∠DAE的度数为 如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.
如图,在△ABC中,AB=AC,D是△ABC内一点,且BD=DC.求证:∠ABD=∠ACD.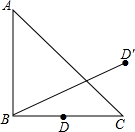 如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′=
如图,在△ABC中,AB=BC,∠ABC=90°,D是BC的中点,且它关于AC的对称点是D′,BD′= 如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有
如图,在△ABC中,AB=AC,D点是BC的中点,DE⊥AB于E点,DF⊥AC于F点,则图中全等三角形共有