题目内容
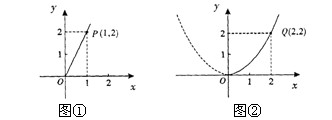
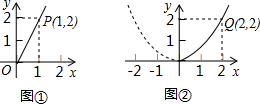 随着我市近几年城市园林绿化建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资成本x成正比例关系,如图①所示;种植花卉的利润y2与投资成本x成二次函数关系,如图②所示.(注:利润与投资成本的单位:万元)
随着我市近几年城市园林绿化建设的快速发展,对花木的需求量逐年提高.某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资成本x成正比例关系,如图①所示;种植花卉的利润y2与投资成本x成二次函数关系,如图②所示.(注:利润与投资成本的单位:万元)(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户计划以8万元资金投入种植花卉和树木,请求出他所获得的总利润Z与投入种植花卉的投资量x之间的函数关系式,并回答他至少获得多少利润?他能获取的最大利润是多少?
分析:(1)设出一次函数解析式和顶点为原点的二次函数解析式,把P,Q分别代入两个函数解析式可得相应的函数解析式;
(2)总利润=种植花卉的利润+种植树木的利润,用公式法可得二次函数的最值问题.
(2)总利润=种植花卉的利润+种植树木的利润,用公式法可得二次函数的最值问题.
解答:解:(1)设y1=kx,由图①所示,函数y1=kx的图象过(1,2),
所以2=k•1,k=2,
故利润y1关于投资量x的函数关系式是y1=2x,
∵该抛物线的顶点是原点,
∴设y2=ax2,
由图②所示,函数y2=ax2的图象过(2,2),
∴2=a•22,即a=
,
故利润y2关于投资量x的函数关系式是:y2=
x2;
(2)设这位专业户投入种植花卉x万元(0≤x≤8),则投入种植树木(8-x)万元,他获得的利润是z万元,根据题意,得z=2(8-x)+
x2=
x2-2x+16=
(x-2)2+14,
当x=2时,z的最小值是14,
∵0≤x≤8,
∴当x=8时,z的最大值是32.
所以2=k•1,k=2,
故利润y1关于投资量x的函数关系式是y1=2x,
∵该抛物线的顶点是原点,
∴设y2=ax2,
由图②所示,函数y2=ax2的图象过(2,2),
∴2=a•22,即a=
| 1 |
| 2 |
故利润y2关于投资量x的函数关系式是:y2=
| 1 |
| 2 |
(2)设这位专业户投入种植花卉x万元(0≤x≤8),则投入种植树木(8-x)万元,他获得的利润是z万元,根据题意,得z=2(8-x)+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x=2时,z的最小值是14,
∵0≤x≤8,
∴当x=8时,z的最大值是32.
点评:考查二次函数的应用;求函数解析式通常用待定系数法;掌握函数的图象的特点是解决本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目