题目内容
若(2x+3)2和
互为相反数,求x-y的值.
| y+2 |
分析:根据互为相反数的两个数的和等于0列出等式,再根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.
解答:解:∵(2x+3)2和
互为相反数,
∴(2x+3)2+
=0,
∴2x+3=0,y+2=0,
解得x=-
,y=-2,
所以,x-y=-
-(-2)=-
+2=
.
| y+2 |
∴(2x+3)2+
| y+2 |
∴2x+3=0,y+2=0,
解得x=-
| 3 |
| 2 |
所以,x-y=-
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
若不等式2x-1<10和x+3>6都成立,那么x满足( )
| A、x>3 | ||
B、x<
| ||
C、3<x<
| ||
D、x<3或x>
|
若(2x-3)2和
互为相反数,则xy的值是( )
| y+2 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
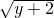 互为相反数,则xy的值是
互为相反数,则xy的值是


 互为相反数,则xy的值是( )
互为相反数,则xy的值是( )


