题目内容
公路上有两辆匀速行驶的汽车,甲汽车在乙汽车前方a千米处,甲汽车在C地,乙汽车在A地,两车同时出发前往距A地900千米的B地,已知乙汽车由A地到B地共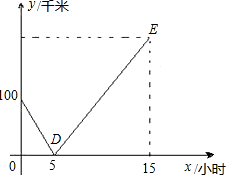 用了15小时.设甲汽车行驶的时间为x小时,行驶中两车的距离为 y千米,y与x的函数关系如图所示:
用了15小时.设甲汽车行驶的时间为x小时,行驶中两车的距离为 y千米,y与x的函数关系如图所示:
根据图象进行探究:
信息读取
(1)出发前,甲汽车在乙汽车前方a=________千米;
(2)解释图中点D的实际意义;
图象理解
(3)分别求出甲汽车和乙汽车的速度;
(4)求E点的坐标.
解:(1)∵图象经过点(0,100)
∴出发前,甲汽车在乙汽车前方a=100千米;
(2)D处的含义:同时出发5小时后,乙汽车追上了甲汽车;
(3)∵两地相距900千米,乙车用时15小时行完,
∴900÷15=60千米/小时
设甲车每小时行驶x千米,
∴5(60-x)=100,
解得:x=40,
∴甲每小时行驶40千米;乙每小时行驶60千米;
(4)∵15小时乙共行驶了900千米,甲行驶了600千米,
∴两车相距300千米,
300-100=200千米
∴E(15,200).
分析:(1)根据函数的图象可知纵坐标表示两车之间的距离,当时间为0时,纵坐标为100即可得到答案;
(2)D点的纵坐标为0可知两车之间的距离为0;
(3)根据两地之间的距离和乙车所用时间可以求出乙车的速度,根据乙车5小时追上甲车可以求出甲的速度;
(4)15小时后乙到达目的地共行驶了的距离减去甲行驶的距离即可得到E的纵坐标;
点评:本题考查了一次函数的综合知识,解决此题的关键是从实际问题中整理出一次函数模型并应用一次函数的知识解题.
∴出发前,甲汽车在乙汽车前方a=100千米;
(2)D处的含义:同时出发5小时后,乙汽车追上了甲汽车;
(3)∵两地相距900千米,乙车用时15小时行完,
∴900÷15=60千米/小时
设甲车每小时行驶x千米,
∴5(60-x)=100,
解得:x=40,
∴甲每小时行驶40千米;乙每小时行驶60千米;
(4)∵15小时乙共行驶了900千米,甲行驶了600千米,
∴两车相距300千米,
300-100=200千米
∴E(15,200).
分析:(1)根据函数的图象可知纵坐标表示两车之间的距离,当时间为0时,纵坐标为100即可得到答案;
(2)D点的纵坐标为0可知两车之间的距离为0;
(3)根据两地之间的距离和乙车所用时间可以求出乙车的速度,根据乙车5小时追上甲车可以求出甲的速度;
(4)15小时后乙到达目的地共行驶了的距离减去甲行驶的距离即可得到E的纵坐标;
点评:本题考查了一次函数的综合知识,解决此题的关键是从实际问题中整理出一次函数模型并应用一次函数的知识解题.

练习册系列答案
相关题目
 23、公路上有两辆匀速行驶的汽车,甲汽车在乙汽车前方a千米处,甲汽车在C地,乙汽车在A地,两车同时出发前往距A地900千米的B地,已知乙汽车由A地到B地共用了15小时.设甲汽车行驶的时间为x小时,行驶中两车的距离为 y千米,y与x的函数关系如图所示:
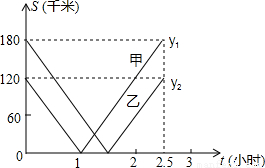
23、公路上有两辆匀速行驶的汽车,甲汽车在乙汽车前方a千米处,甲汽车在C地,乙汽车在A地,两车同时出发前往距A地900千米的B地,已知乙汽车由A地到B地共用了15小时.设甲汽车行驶的时间为x小时,行驶中两车的距离为 y千米,y与x的函数关系如图所示: 一条笔直的公路上依次有B、A、C三地,BC两地相距300千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(千米)与行驶时间t(时)的关系如图所示,则甲、乙两车相遇时离A地的距离为
一条笔直的公路上依次有B、A、C三地,BC两地相距300千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(千米)与行驶时间t(时)的关系如图所示,则甲、乙两车相遇时离A地的距离为