题目内容
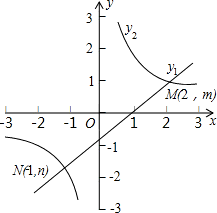 如图,函数y1=kx+b和函数y2=
如图,函数y1=kx+b和函数y2= 图象相交于点M(2,m),N(-1,n),若
图象相交于点M(2,m),N(-1,n),若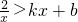 ,则x的取值范围是
,则x的取值范围是
- A.x<-1或0<x<2
- B.x<-1或x>2
- C.-1<x<0或0<x<2
- D.-1<x<0或x>2
A
分析:观察图象得到当x<-1或x>2时,函数y1=kx+b的函数图象都在函数y2= 的图象的上方,即有
的图象的上方,即有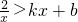 .
.
解答:∵函数y1=kx+b和函数y2= 图象相交于点M(2,m),N(-1,n),
图象相交于点M(2,m),N(-1,n),
∴当x<-1或x>2时,函数y1=kx+b的函数图象都在函数y2= 的图象的上方,
的图象的上方,
∴当x<-1或x>2时,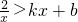 .
.
故选A.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数解析式.也考查了观察函数图象的能力.
分析:观察图象得到当x<-1或x>2时,函数y1=kx+b的函数图象都在函数y2=
 的图象的上方,即有
的图象的上方,即有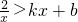 .
.解答:∵函数y1=kx+b和函数y2=
 图象相交于点M(2,m),N(-1,n),
图象相交于点M(2,m),N(-1,n),∴当x<-1或x>2时,函数y1=kx+b的函数图象都在函数y2=
 的图象的上方,
的图象的上方,∴当x<-1或x>2时,
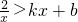 .
.故选A.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标同时满足两个函数解析式.也考查了观察函数图象的能力.

练习册系列答案
相关题目
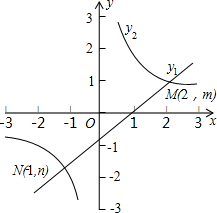 如图,函数y1=kx+b和函数y2=
如图,函数y1=kx+b和函数y2= 如图,一次函数y1=kx+b的图象与反比例函数
如图,一次函数y1=kx+b的图象与反比例函数 如图,函数y1=kx+b和函数y2=
如图,函数y1=kx+b和函数y2= 图象相交于点M(2,m),N(-1,n),若
图象相交于点M(2,m),N(-1,n),若 ,则x的取值范围是( )
,则x的取值范围是( ) 如图,函数y1=kx+b和函数y2=
如图,函数y1=kx+b和函数y2= 图象相交于点M(2,m),N(-1,n),若
图象相交于点M(2,m),N(-1,n),若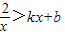 ,则x的取值范围是( )
,则x的取值范围是( )