题目内容
【题目】如图,在△ABC中,AB=AC,BC=12,sinC=![]() ,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.
,点G是△ABC的重心,线段BG的延长线交边AC于点D,求∠CBD的余弦值.

【答案】cos∠CBD=![]()
【解析】试题分析:
如下图,连接AG并延长交BC于点H,由已知条件易得BH=CH=6,AG=2GH,AH⊥BC于点H,由sinC=![]() 设AH=4k,则AC=5k结合CH=6在Rt△ACH中由勾股定理可得关于k的方程,解方程可得k=2,从而可得AH=8,AC=10,则GH=
设AH=4k,则AC=5k结合CH=6在Rt△ACH中由勾股定理可得关于k的方程,解方程可得k=2,从而可得AH=8,AC=10,则GH=![]() ,结合BH=6即可的BG的长,从而在Rt△BHG中即可求得cos∠CBD的值了.
,结合BH=6即可的BG的长,从而在Rt△BHG中即可求得cos∠CBD的值了.
试题解析:
如图连接AG延长AG交BC于H.
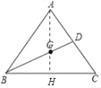
∵G是重心,
∴BH=CH=6,AG=2GH,
∵AB=AC,
∴AH⊥BC,
∵sin∠C=![]() ,设AH=4k,AC=5k,
,设AH=4k,AC=5k,
在Rt△AHC中,∵AH2+CH2=AC2,
∴(4k)2+62=(5k)2,
解得k=2,
∴AH=8,AC=10,
∴GH=![]() ,
,
在Rt△BGH中,BG=![]() ,
,
∴cos∠CBD=![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目