题目内容
计算12-22+32-42+52-62+…+19992的值是
- A.199000
- B.-199000
- C.1999
- D.-1999
A
分析：利用平方差公式先进行展开，然后再求和，从而进行解．
解答：12-22+32-42+52-62+…+19992=12+32-22+52-42+…+19992-19982
=1+1×5+1×9+1×13+…+1×3997
=1+
=1+2001×999
=199000，
故选A．
点评：此题主要考查平方差公式的性质及其应用，有一定的难度，计算时要仔细．
分析：利用平方差公式先进行展开，然后再求和，从而进行解．
解答：12-22+32-42+52-62+…+19992=12+32-22+52-42+…+19992-19982
=1+1×5+1×9+1×13+…+1×3997
=1+
=1+2001×999
=199000，
故选A．
点评：此题主要考查平方差公式的性质及其应用，有一定的难度，计算时要仔细．
练习册系列答案
阅读快车系列答案
相关题目
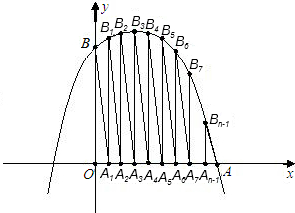S2、S3、S4、…、Sn．