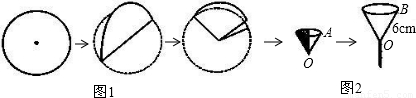
题目内容
在化学实验中,小明将半径为6cm的圆形滤纸片按图1所示的步骤进行折叠,并围成圆锥形.取一漏斗,上部的圆锥形内壁(忽略漏斗管口处)的母线OB长为6cm,开口直径为6cm.当滤纸片重叠部分三层,且每层为| 1 | 4 |
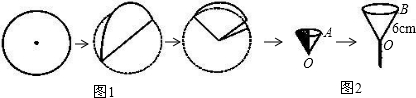
分析:此题是圆锥侧面积求解的典型问题,要灵活运用公式,并结合实际解题.
解答: 解:∵表面紧贴的两圆锥形的侧面展开图为圆心角相同的两扇形,
解:∵表面紧贴的两圆锥形的侧面展开图为圆心角相同的两扇形,
∴表面是否紧贴只需考虑展开图的圆心角是否相等.
由于滤纸围成的圆锥形只有最外层侧面紧贴漏斗内壁,故只考虑该滤纸圆锥最外层的侧面和漏斗内壁圆锥侧面的关系.
将圆形滤纸片按图示的步骤折成四层且每层为
圆,
则围成的圆锥形的侧面积=(1-2×
)S滤纸圆=
S滤纸圆.
∴它的侧面展开图是半圆,其圆心角为180度,
如将漏斗内壁构成的圆锥侧面也抽象地展开,展开的扇形弧长为π×6=6π(cm),
该侧面展开图的圆心角为6π÷6×
=180度.
由此可以看出两圆锥的侧面展开得到的扇形,它们的圆心角相等.
∴该滤纸围成的圆锥形必能紧贴漏斗内壁.
 解:∵表面紧贴的两圆锥形的侧面展开图为圆心角相同的两扇形,
解:∵表面紧贴的两圆锥形的侧面展开图为圆心角相同的两扇形,∴表面是否紧贴只需考虑展开图的圆心角是否相等.
由于滤纸围成的圆锥形只有最外层侧面紧贴漏斗内壁,故只考虑该滤纸圆锥最外层的侧面和漏斗内壁圆锥侧面的关系.
将圆形滤纸片按图示的步骤折成四层且每层为
| 1 |
| 4 |
则围成的圆锥形的侧面积=(1-2×
| 1 |
| 4 |
| 1 |
| 2 |
∴它的侧面展开图是半圆,其圆心角为180度,
如将漏斗内壁构成的圆锥侧面也抽象地展开,展开的扇形弧长为π×6=6π(cm),
该侧面展开图的圆心角为6π÷6×
| 180° |
| π |
由此可以看出两圆锥的侧面展开得到的扇形,它们的圆心角相等.
∴该滤纸围成的圆锥形必能紧贴漏斗内壁.
点评:本题考查了圆锥的计算,将几何图形做适当变形,找出隐藏条件是解一些复杂几何问题常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 圆时,滤纸围成的圆锥形放入该漏斗中,能否紧贴漏斗的内壁?请你用所学的数学知识说明.
圆时,滤纸围成的圆锥形放入该漏斗中,能否紧贴漏斗的内壁?请你用所学的数学知识说明.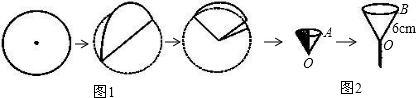
 圆时,滤纸围成的圆锥形放入该漏斗中,能否紧贴漏斗的内壁?请你用所学的数学知识说明.
圆时,滤纸围成的圆锥形放入该漏斗中,能否紧贴漏斗的内壁?请你用所学的数学知识说明.