题目内容
11.函数y=$\sqrt{x-2}$中,自变量x的取值范围是x≥2;实数2-$\sqrt{3}$的倒数是2+$\sqrt{3}$.分析 根据被开方数是非负数,倒数的定义,可得答案.
解答 解:y=$\sqrt{x-2}$中,自变量x的取值范围是 x≥2;
实数2-$\sqrt{3}$的倒数是 2+$\sqrt{3}$,
故答案为:x≥2,2+$\sqrt{3}$.
点评 本题考查了函数自变量的取值范围,利用被开方数是非负数得出不等式是解题关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
2.下列说法正确的是( )
| A. | 连续抛一枚硬币n次,当n越来越大时,出现正面朝上的频率会越来越稳定于0.5 | |
| B. | 连续抛一枚硬币50次,出现正面朝上的次数是25次 | |
| C. | 连续三次掷一颗骰子都出现了奇数,则第四次出现的数一定是偶数 | |
| D. | 某地发行一种福利彩票,中奖概率为1%,买这种彩票100张一定会中奖 |
6.在平面直角坐标系中,⊙P的半径是2,点P(0,m)在y轴上移动,当⊙P与x轴相交时,m的取值范围是( )
| A. | m<2 | B. | m>2 | C. | m>2或m<-2 | D. | -2<m<2 |
16.下列分解因式正确的是( )
| A. | x3-x=x(x2-1) | B. | m2+m-7=(m+3)(m-2)-1 | C. | (a+4)(a-4)=a2-16 | D. | x2-y2=(x+y)(x-y) |
 如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为点E,过点C作DA的平行线与AF相交于点F,CD=4$\sqrt{3}$,BE=2.
如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为点E,过点C作DA的平行线与AF相交于点F,CD=4$\sqrt{3}$,BE=2.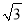 ,则它的边长为( )
,则它的边长为( ) D. 4
D. 4