题目内容
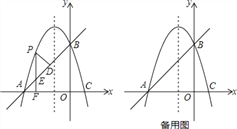
【题目】如图1,在直角坐标系中放入一个边长AB长为3,BC长为5的矩形纸片ABCD,使得BC、AB所在直线分别与x、y轴重合.将纸片沿着折痕AE翻折后,点D恰好落在x轴上,记为F.

(1)求折痕AE所在直线与x轴交点的坐标;
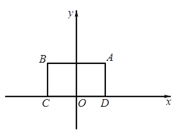
(2)如图2,过D作DG⊥AF,求DG的长度;
(3)将矩形ABCD水平向右移动n个单位,则点B坐标为(n,0),其中n>0.如图3所示,连接OA,若△OAF是等腰三角形,试求点B的坐标.
【答案】(1)折痕AE所在直线与x轴交点的坐标为(9,0);(2)3;(3)点B(4,0)或B(1,0).
【解析】
(1)根据四边形ABCD是矩形以及由折叠对称性得出AF=AD=5,EF=DE,进而求出BF的长,即可得出E点的坐标,进而得出AE所在直线与x轴交点的坐标;
(2)判断出△DAG≌△AFB,即可得出结论;
(3)分三种情况讨论:若AO=AF,OF=FA,AO=OF,利用勾股定理求出即可.
解:(1)∵四边形ABCD是矩形,
∴AD=CB=5,AB=DC=3,∠D=∠DCB=∠ABC=90°,
由折叠对称性:AF=AD=5,EF=DE,
在Rt△ABF中,BF=![]() =4,
=4,
∴CF=1,
设EC=x,则EF=3﹣x,
在Rt△ECF中,12+x2=(3﹣x)2,
解得:x=![]() ,
,
∴E点坐标为:(5,![]() ),
),
∴设AE所在直线解析式为:y=ax+b,
则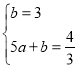 ,
,
解得: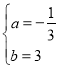 ,
,
∴AE所在直线解析式为:y=![]() x+3,
x+3,
当y=0时,x=9,
故折痕AE所在直线与x轴交点的坐标为:(9,0);
(2)在△DAG和△AFB中
∵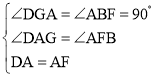 ,
,
∴△DAG≌△AFB,
∴DG=AB=3;
(3)分三种情况讨论:
若AO=AF,
∵AB⊥OF,
∴BO=BF=4,
∴n=4,
∴B(4,0),
若OF=FA,则n+4=5,
解得:n=1,
∴B(1,0),
若AO=OF,
在Rt△AOB中,AO2=OB2+AB2=m2+9,
∴(n+4)2=n2+9,
解得:n=![]() (n<0不合题意舍去),
(n<0不合题意舍去),
综上所述,若△OAF是等腰三角形,n的值为n=4或1.
即点B(4,0)或B(1,0).

 名校课堂系列答案
名校课堂系列答案