题目内容
5、请找出下图圆中的圆心，并写出你找圆心的方法．（不要求证明）分析：弦的垂直平分线必过圆心，那么做出圆上的任意两条弦的垂直平分线的交点即为圆心．
解答：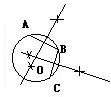
解：（1）在圆上任取三点A、B、C，
（2）连AB、BC，
（3）作线段AB的垂直平分线EF，
（4）作线段BC的垂直平分线MN，与EF交于O点．
则O点即为该圆的圆心．
解：（1）在圆上任取三点A、B、C，（2）连AB、BC，
（3）作线段AB的垂直平分线EF，
（4）作线段BC的垂直平分线MN，与EF交于O点．
则O点即为该圆的圆心．
点评：用到的知识点为：圆上任意两条弦的垂直平分线的交点即为圆心．
练习册系列答案
阅读快车系列答案
相关题目
请找出下图圆中的圆心，并写出你找圆心的方法．（不要求证明）
