题目内容

如图，是两个可以自由转动的圆盘，被分成若干个相等的扇形，分别转动圆盘，停止后，指针指向红色区域的概率是多大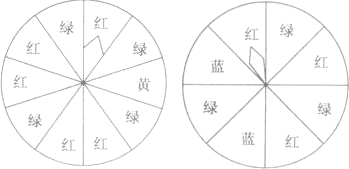？精英家教网
分析：本题应首先根据红色区域在整个圆盘中所占的份数分别计算在每个圆盘中指针指向红色区域的概率，然后再把这两个概率相乘，即为所求的概率．
解答：解：∵两个可以自由转动的圆盘，被分成若干个相等的扇形，
∴由图可知：在上边的图形中红色区域占5份，共有10份，
则停止后，指针指向红色区域的概率是
5
10
=
1
2
；
对下图来说，红色区域占3份，共有8份，
则停止后，指针指向红色区域的概率是
3
8
；
综上可知：则停止后，指针指向红色区域的概率是
1
2
×
3
8
=
3
16
．
点评：本题主要考查了几何概率，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
如图，是两个可以自由转动的均匀转盘A，B，转盘A被分成4等份，每份分别标上1，2，3，4四个数字；转盘B被分成6等份，每份分别标上1，2，3，4，5，6六个数字，现为甲，乙两人设计一个游戏，其规则如下：
①同时自由转盘转盘A，B；
②转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止），用所指的两个数字相乘．如果得到的积是偶数，那么甲胜；如果得到的积是奇数，则乙胜．
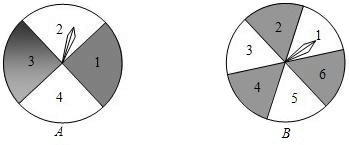你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则精英家教网，并说明道理．
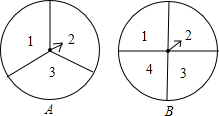精英家教网如图，是两个可以自由转动的转盘，每个转盘被分成两个扇形，同时转动两个转盘，转盘停止后，指针所指区域内的数字之和为4的概率是
 
．
精英家教网如图，是两个可以自由转动的均匀圆盘A和B，A、B分别被均匀的分成三等份和四等份．同时自由转动圆盘A和B，圆盘停止后，指针分别指向的两个数字的积为偶数的概率是（　　）
A、
3
4
B、
2
3
C、
1
2
D、
1
3
（2012•德州一模）如图，是两个可以自由转动的均匀圆盘A和B，A、B分别被均匀的分成三等份和四等份．同时自由转动圆盘A和B，圆盘停止后，指针分别指向的两个数字的积为偶数的概率是
2
3
2
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网