题目内容
下列因式分解的变形中,正确的是
- A.x2-(a+1)x+a2=(x-1)(x-a)
- B.
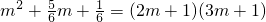
- C.y2+(a2+b2)•y+a2b2=(y+a2)(y+b2)
- D.(x2-3x)2-2(x2-3x)-8=(x-1)(x-2)(x+4)(x-1)
C
分析:利用十字相乘法进行因式分解,同时注意因式分解是恒等变形,再逐个检验.
解答:A、假设x2-(a+1)x+a2=(x-1)(x-a)成立,进一步化简可得a2=a,所以,不正确;
B、假设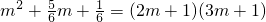 成立,右式=6m2+5m+1,可见左式≠右式;
成立,右式=6m2+5m+1,可见左式≠右式;
C、y2+(a2+b2)•y+a2b2=(y+a2)(y+b2)符合十字相乘法的条件.
D、(x2-3x)2-2(x2-3x)-8=[(x2-3x)-4][(x2-3x)+2]=(x-4)(x+1)(x-2)(x-1),可见左式≠右式
故选C
点评:利用十字相乘法进行因式分解,对于多项式中次数较多的可多次使用十字相乘法.
分析:利用十字相乘法进行因式分解,同时注意因式分解是恒等变形,再逐个检验.
解答:A、假设x2-(a+1)x+a2=(x-1)(x-a)成立,进一步化简可得a2=a,所以,不正确;
B、假设
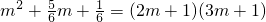 成立,右式=6m2+5m+1,可见左式≠右式;
成立,右式=6m2+5m+1,可见左式≠右式;C、y2+(a2+b2)•y+a2b2=(y+a2)(y+b2)符合十字相乘法的条件.
D、(x2-3x)2-2(x2-3x)-8=[(x2-3x)-4][(x2-3x)+2]=(x-4)(x+1)(x-2)(x-1),可见左式≠右式
故选C
点评:利用十字相乘法进行因式分解,对于多项式中次数较多的可多次使用十字相乘法.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
下列因式分解的变形中,正确的是( )
| A、x2-(a+1)x+a2=(x-1)(x-a) | ||||
B、m2+
| ||||
| C、y2+(a2+b2)•y+a2b2=(y+a2)(y+b2) | ||||
| D、(x2-3x)2-2(x2-3x)-8=(x-1)(x-2)(x+4)(x-1) |