题目内容
若一直角三角形两直角边的长分别为 ,
, ,则这个直角三角形斜边上的高线为________.
,则这个直角三角形斜边上的高线为________.

分析:根据勾股定理求得该直角三角形的斜边长,然后由三角形的面积公式即可求得直角三角形斜边上的高线的长度.
解答:∵一直角三角形两直角边的长分别为
 ,
, ,
,∴根据勾股定理知该直角三角形的斜边长度为:
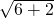 =2
=2 ;
;设该直角三角形斜边上的高线为h,则
 ×
× ×
× =
= ×2
×2 ×h,
×h,解得h=
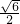 .
.故答案是:
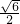 .
.点评:本题考查了勾股定理.解题时,借用了直角三角形的“等积转换”的知识.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目