题目内容
 附加题
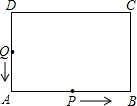
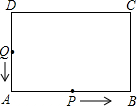
附加题如图,在长方形ABCD中,AB=14cm,AD=8cm,动点P沿AB边从点A开始,向点B以1cm/s的速度运动;动点Q从点D开始沿DA→AB边,向点B以2cm/s的速度运动.P,Q同时开始运动,当点Q到达B点时,点P和点Q同时停止运动,用t(s)表示运动的时间.
(1)当点Q在DA边上运动时,t为何值,使AQ=AP?
(2)当t为何值时,AQ+AP等于长方形ABCD周长的
| 1 | 4 |
(3)当t为何值时,点Q能追上点P?
分析:(1)分别用t表示出点Q在DA边上运动时AQ和AP的长,再根据AQ=AP,列出方程求解即可;
(2)分两种情况:点Q在DA边上;点Q在AB边上;根据AQ+AP等于长方形ABCD周长的
,列出方程求解即可;
(3)根据路程差等于8,列出方程即可求解.
(2)分两种情况:点Q在DA边上;点Q在AB边上;根据AQ+AP等于长方形ABCD周长的
| 1 |
| 4 |
(3)根据路程差等于8,列出方程即可求解.
解答:解:(1)依题意有:8-2t=t,
解得t=
,
故当点Q在DA边上运动时,t为
s时,使AQ=AP;
(2)(14+8)×2×
=11(cm).
①点Q在DA边上时,
依题意有:8-2t+t=11,
解得t=-3(不合题意舍去)
②点Q在AB边上时,
依题意有:2t-8+t=11,
解得t=
.
故当t为
时,AQ+AP等于长方形ABCD周长的
;
(3)依题意有:2t-t=8,
解得t=8.
故当t为8s时,点Q能追上点P.
解得t=
| 8 |
| 3 |
故当点Q在DA边上运动时,t为
| 8 |
| 3 |
(2)(14+8)×2×
| 1 |
| 4 |
①点Q在DA边上时,
依题意有:8-2t+t=11,
解得t=-3(不合题意舍去)
②点Q在AB边上时,
依题意有:2t-8+t=11,
解得t=
| 19 |
| 3 |
故当t为
| 19 |
| 3 |
| 1 |
| 4 |
(3)依题意有:2t-t=8,
解得t=8.
故当t为8s时,点Q能追上点P.
点评:此题考查动点移动问题,主要是一元一次方程的性质及其应用,解题的关键是根据等量关系列出方程求出t值.

练习册系列答案
相关题目
 附加题
附加题 ?
?