题目内容
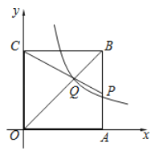
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为4,顶点
的边长为4,顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,抛物线
轴上,抛物线![]() 经过点D(-1,0).
经过点D(-1,0).
(1)求点C的坐标;
(2)求抛物线的对称轴;
(3)若抛物线![]() 与正方形
与正方形![]() 的边恰好有三个公共点,求
的边恰好有三个公共点,求![]() 的值.
的值.

【答案】(1)C(0,4).(2)![]() .(3)
.(3)![]() ,
,![]() .
.
【解析】
(1)根据正方形的性质,直接读图可得;
(2)将点D代入抛物线,利用对称轴公式求解可得;
(3)存在2种情况,都可确定抛物线上一点坐标,代入即可得![]() 的值.
的值.
(1)∵正方OABC的边长为4,B(4,4)
∴C(0,4)
(2)将点D(-1,0)代入抛物线得:0= ![]() -b-3
-b-3![]()
化简得:b=-2![]()
抛物线的对称轴为:x=![]()
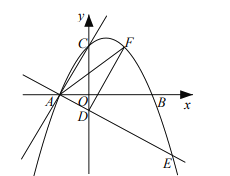
(3)情况一:如下图,抛物线顶点恰好在正方形CB边长
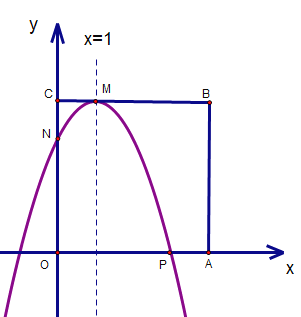
即抛物线过点M(1,4)
已知抛物线过点D(-1,0),将这两点代入,解得:![]() ,
,![]() =-1
=-1
情况二:如下图,抛物线与y轴的交点恰好是点C
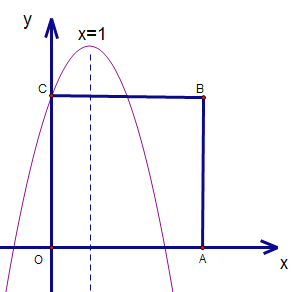
即抛物线过点C(0,4)
已知抛物线过点D(-1,0),将这两点代入,解得:![]() ,
,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目