题目内容
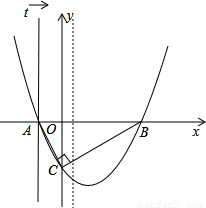
如图,在平面直角示系中,A、B两点的坐标分别是A(-1,0)、B(4,0),点C在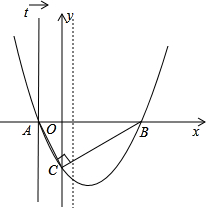 y轴的负半轴上,且∠ACB=90°
y轴的负半轴上,且∠ACB=90°(1)求点C的坐标;
(2)求经过A、B、C三点的抛物线的解析式;
(3)直线l⊥x轴,若直线l由点A开始沿x轴正方向以每秒1个单位的速度匀速向右平移,设运动时间为t(0≤t≤5)秒,运动过程中直线l在△ABC中所扫过的面积为S,求S与t的函数关系式.
分析:(1)根据A、B的坐标,可求得OA、OB的长,在Rt△ABC中,OC⊥AB,利用射影定理即可求得OC的值,从而得到C点的坐标.
(2)已知了抛物线上的三点坐标,可利用待定系数法求得抛物线的解析式.
(3)此题应分段考虑:
①当0≤t≤1时,直线l扫过△ABC的部分是个直角三角形,设直线l与AC、AB的交点为M、N,易证得△AMN∽△ACO,根据相似三角形所得比例线段即可求得MN的值,从而利用三角形的面积公式求得S、t的函数关系式;
②当1<t≤5时,直线l扫过△ABC的部分是个多边形,设直线l与BC、AB的交点为M、N,同①可求得MN的长,即可得到△BMN的面积表达式,那么△ACB、△BMN的面积差即为直线l扫过部分的面积,由此求得S、t的函数关系式.
(2)已知了抛物线上的三点坐标,可利用待定系数法求得抛物线的解析式.
(3)此题应分段考虑:
①当0≤t≤1时,直线l扫过△ABC的部分是个直角三角形,设直线l与AC、AB的交点为M、N,易证得△AMN∽△ACO,根据相似三角形所得比例线段即可求得MN的值,从而利用三角形的面积公式求得S、t的函数关系式;
②当1<t≤5时,直线l扫过△ABC的部分是个多边形,设直线l与BC、AB的交点为M、N,同①可求得MN的长,即可得到△BMN的面积表达式,那么△ACB、△BMN的面积差即为直线l扫过部分的面积,由此求得S、t的函数关系式.
解答:解:(1)已知A(-1,0),B(4,0),则OA=1,OB=4;
在Rt△ABC中,CO⊥AB,
由射影定理得:OC2=OA•OB=4,
即OC=2,
故C(0,-2).
(2)设抛物线的解析式为:y=a(x+1)(x-4),
依题意有:a(0+1)(0-4)=-2,a=
,
故抛物线的解析式为:y=
(x+1)(x-4)=
x2-
x-2.
(3)①当0≤t≤1时,由题意知:AM=t;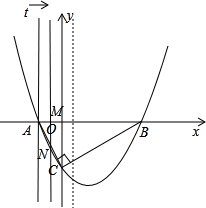
∵直线l∥OC,且OC=2OA,
∴MN=2AM=2t;
故S=
t•2t=t2;
②当1<t≤5时,由于AM=t,AB=5,则BM=5-t;
∵直线l∥OC,且OB=2OC,
∴MN=
BM=
,
故S=
×5×2-
×
=-
t2+
t-
;
综上可知:S、t的函数关系式为:
S=
.
在Rt△ABC中,CO⊥AB,
由射影定理得:OC2=OA•OB=4,
即OC=2,
故C(0,-2).
(2)设抛物线的解析式为:y=a(x+1)(x-4),
依题意有:a(0+1)(0-4)=-2,a=
| 1 |
| 2 |
故抛物线的解析式为:y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)①当0≤t≤1时,由题意知:AM=t;

∵直线l∥OC,且OC=2OA,
∴MN=2AM=2t;
故S=
| 1 |
| 2 |
②当1<t≤5时,由于AM=t,AB=5,则BM=5-t;
∵直线l∥OC,且OB=2OC,
∴MN=
| 1 |
| 2 |
| 5-t |
| 2 |
故S=
| 1 |
| 2 |
| 1 |
| 2 |
| (5-t)2 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |
| 5 |
| 4 |
综上可知:S、t的函数关系式为:
S=
|
点评:此题主要考查了直角三角形的性质、相似三角形的性质、二次函数解析式的确定、图形面积的求法等知识;(3)题中,一定要根据直线l的不同位置来分类讨论,以免漏解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
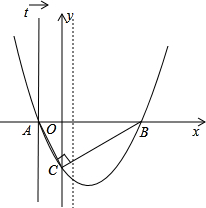 y轴的负半轴上,且∠ACB=90°
y轴的负半轴上,且∠ACB=90°